A wire of 50 cm long, 1mm2 in cross-section carries a current of 4 A, when connected to a 2 V battery, the resistivity of wire is
2×10−7Ωm
5×10−7Ωm
4×10−6Ω m
1×10−6Ωm
The correct Answer is:D
To find the resistivity of the wire, we will follow these steps:
Step 1: Write down the given data
- Length of the wire (L) = 50 cm = 0.5 m
- Cross-sectional area (A) = 1 mm² = 1 x 10⁻⁶ m²
- Current (I) = 4 A
- Voltage (V) = 2 V
Step 2: Calculate the resistance (R) using Ohm's Law
Ohm's Law states that:
R=VI
Substituting the values:
R=2V4A=0.5Ω
Step 3: Use the formula relating resistivity (ρ), resistance (R), length (L), and area (A)
The formula for resistance in terms of resistivity is:
R=ρLA
We can rearrange this to find the resistivity:
ρ=R⋅AL
Step 4: Substitute the values into the formula
Now substituting the values we have:
- R = 0.5 Ω
- A = 1 x 10⁻⁶ m²
- L = 0.5 m
So,
ρ=0.5Ω⋅(1×10−6m2)0.5m
Step 5: Simplify the expression
ρ=0.5×10−60.5
ρ=1×10−6Ω⋅m
Final Answer
The resistivity of the wire is:
ρ=1×10−6Ω⋅m
---
- Length of the wire (L) = 50 cm = 0.5 m
- Cross-sectional area (A) = 1 mm² = 1 x 10⁻⁶ m²
- Current (I) = 4 A
- Voltage (V) = 2 V
Ohm's Law states that:
R=VI
Substituting the values:
R=2V4A=0.5Ω
The formula for resistance in terms of resistivity is:
R=ρLA
We can rearrange this to find the resistivity:
ρ=R⋅AL
Now substituting the values we have:
- R = 0.5 Ω
- A = 1 x 10⁻⁶ m²
- L = 0.5 m
ρ=0.5Ω⋅(1×10−6m2)0.5m
ρ=0.5×10−60.5
ρ=1×10−6Ω⋅m
The resistivity of the wire is:
ρ=1×10−6Ω⋅m
Similar Questions
A long straight wire of circular cross- section carries a current along its length. On the axis inside the wire, it follows that
View SolutionA conductor wire having 1029 free electrons /m3 carries a current of 20A. If the cross-section of the wire is 1mm2, then the drift velocity of electrons will be :
View Solution
Knowledge Check
If a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
A5.34×10−5TB8.34×10−5TC9.6×10−5TD10.2×10−5TA metal rod of the length 10cm and a rectangular cross-section of 1 cm x 1/2 cm is connected to a battery across opposite faces. The resistance will be
Amaximum when the battery is connected acrossBmaximum when the battery is connected acrossCmaximum when the battery is connected acrossDsame irrespective of the three faces.
A battery is connected across a resistance wire of uniform cross-section . If another resistance wire is connected in parallel, then the intensity of electric field in the first wire will
View SolutionA metel rod of the length 10cm and a rectangular cross-section of 1 cm xx 1/2 cm is connected to a battery across opposite faces. The resistance will be
View SolutionA metel rod of the length 10cm and a rectangular cross-section of 1 cm xx 1/2 cm is connected to a battery across opposite faces. The resistance will be
View SolutionA Steel wire is 1mlong and 1mm2 in area of cross-section. If it takes 200N to streach this wire by 1mm, the forces that will be required to stretch the wrie of the same material and cross-sectional area form a length of 10m to 1002cm
View SolutionA wire of given metarial having length l and ares of cross-section A has a resistance of 4Ω. What would be the resistance of another wire of the same meterial having length l/2 and area of cross-section 2A ?
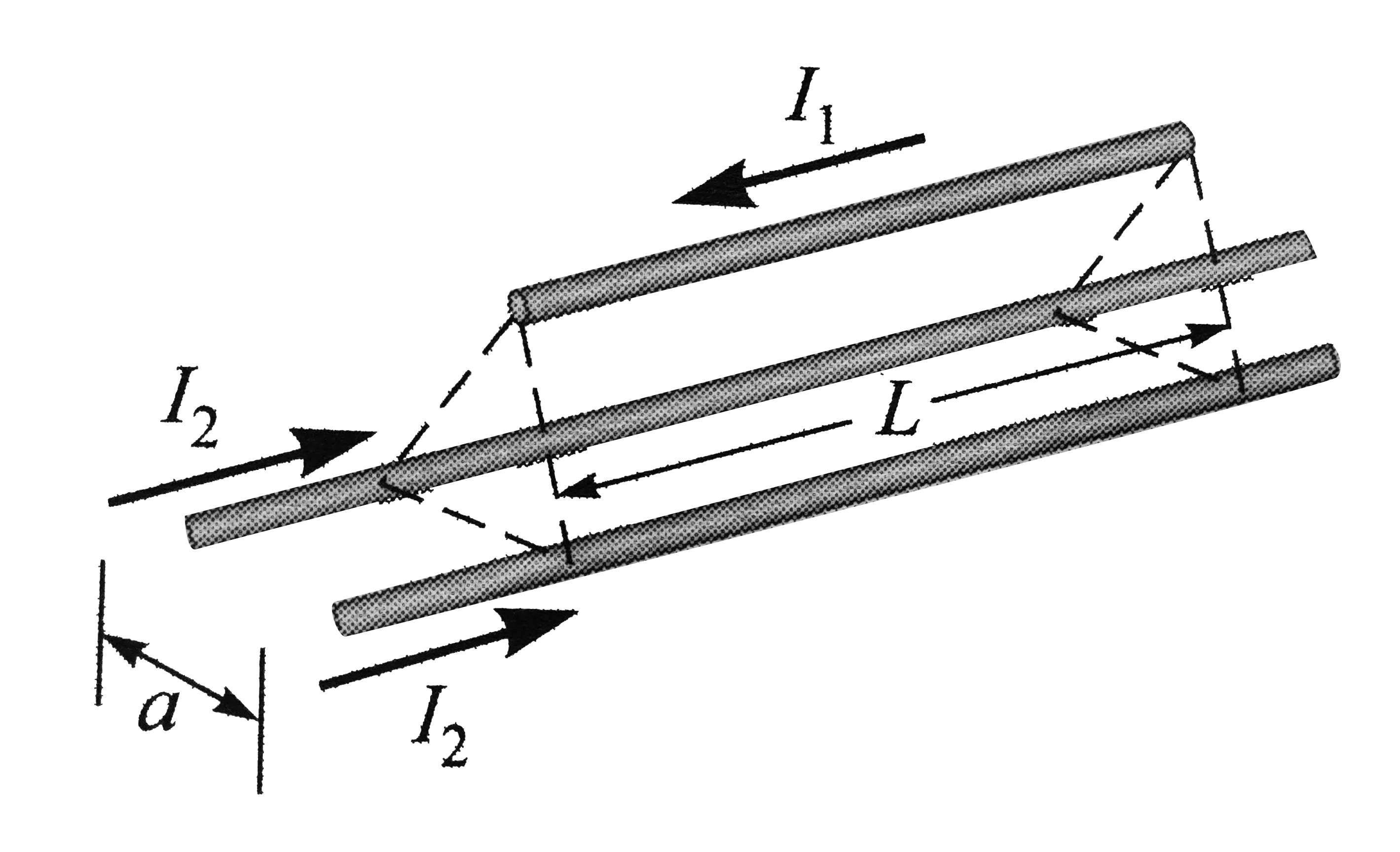
View SolutionTwo infinetely long, parallel wires are lying on the ground at distance a=1cm apart as shown in Fig. A third wire, of length L=10m and mass 400g, carries a current of I1=100A and is levitated above the first two wires, at a horizontal position midway between them. The infinitely long wires carry equal currents I1 in the same directions, but in the direction opposite that in the leviated wire. What current must the infinately long wires carry so that the three wires form an equilateral triangle?

View Solution