Two infinetely long, parallel wires are lying on the ground at distance a=1cm apart as shown in Fig. A third wire, of length L=10m and mass 400g, carries a current of I1=100A and is levitated above the first two wires, at a horizontal position midway between them. The infinitely long wires carry equal currents I1 in the same directions, but in the direction opposite that in the leviated wire. What current must the infinately long wires carry so that the three wires form an equilateral triangle?
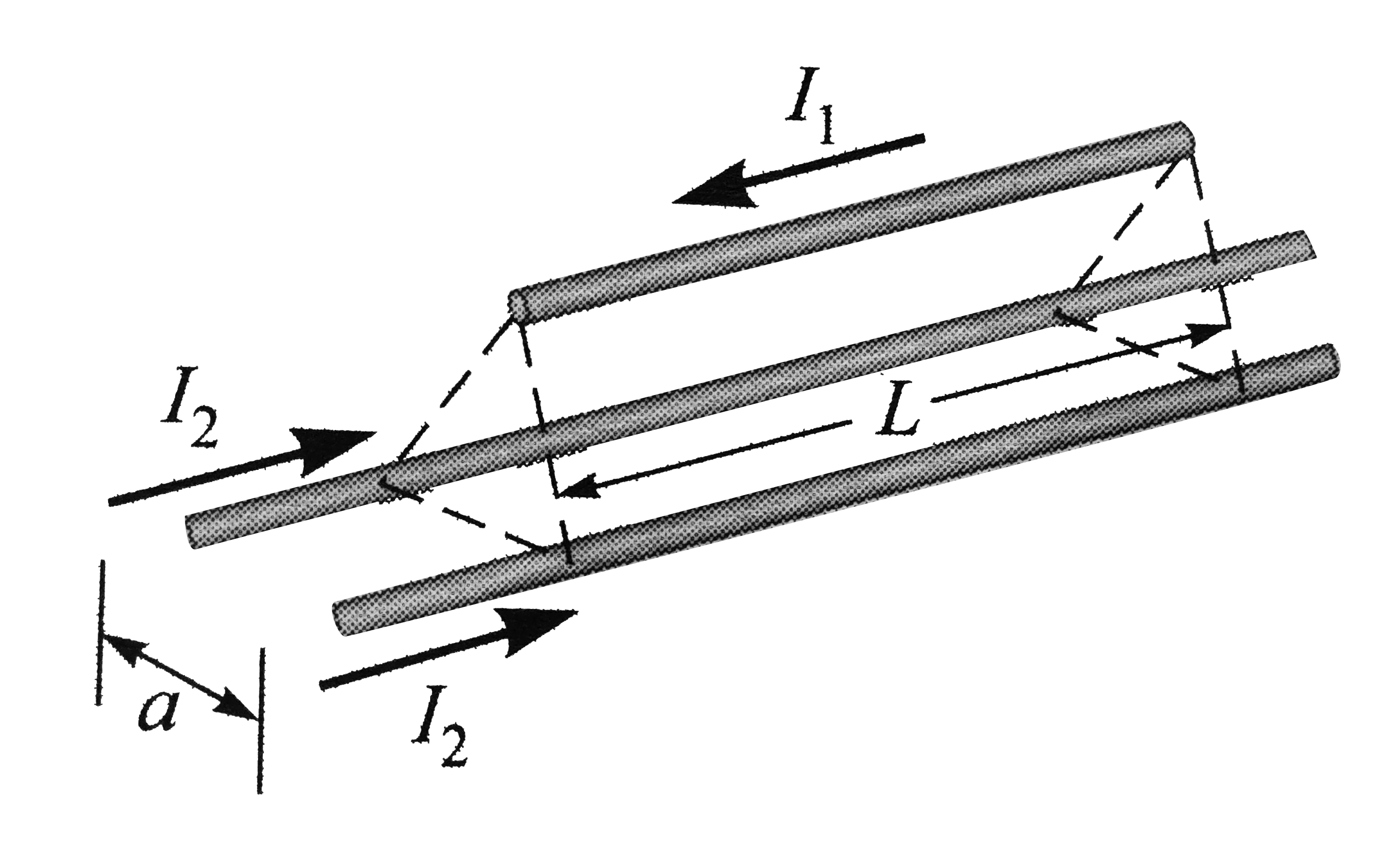

Since the current in the short wire is opposite to those in
the long wires, the short wire is repelled from both of the others.
Imaging the currents in the long wires in Fig are increased.
The repulsive force becomes stronger, and the levitated wire rises to the point at which the wire is once again levitated in
equilibrium at a higher position. Figure shows the desired
situation with the three wires forming an equilateral triangle.
Because the levitated wire is subjected to forces but does not
The horizontal components of the magnetic forces on the levitated
wire cancel. The vertical components are both positive and added
Fig. and in the plane of the page.
The total magnetic force in the upward direction on the levitated
wire:
→FB=2(μ0I1I22πa)cosθˆk=(μ0I1I22πa)lcosθˆk
The gravitational force on the levitaed wire :
→Fg=−mgˆk
Apply the particle in equilibrium model by adding the forces and
setting the net force equal to zero:
Σ→F=→FB+Fg=(μ0I1I2πa)lcosθˆk−mgˆk=0
Solve for the current in the wires on the ground:
I2=mgπaμ0I1lcosθ
Substituting numetical values:
I2=(0.400kg)(10ms−2)π(0.0100m)(4π×10−7T.mA−2)(100A)(10m)cos30∘=113A
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Solved Example
Explore 20 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Concept Exercise 2.1
Explore 35 Videos
- RAY OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:RAY OPTICSExercise:DPP 1.6
Explore 12 Videos
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Comprehension Type
Explore 14 Videos
Similar Questions
Two long wire AB abd CD carry currents i1 and i2 in the direactions show in figure

View SolutionAn infinitely long straight wire is carrying a current I1. Adjacent to it there is another equilateral triangular wire having current I2. Choose the wrong options
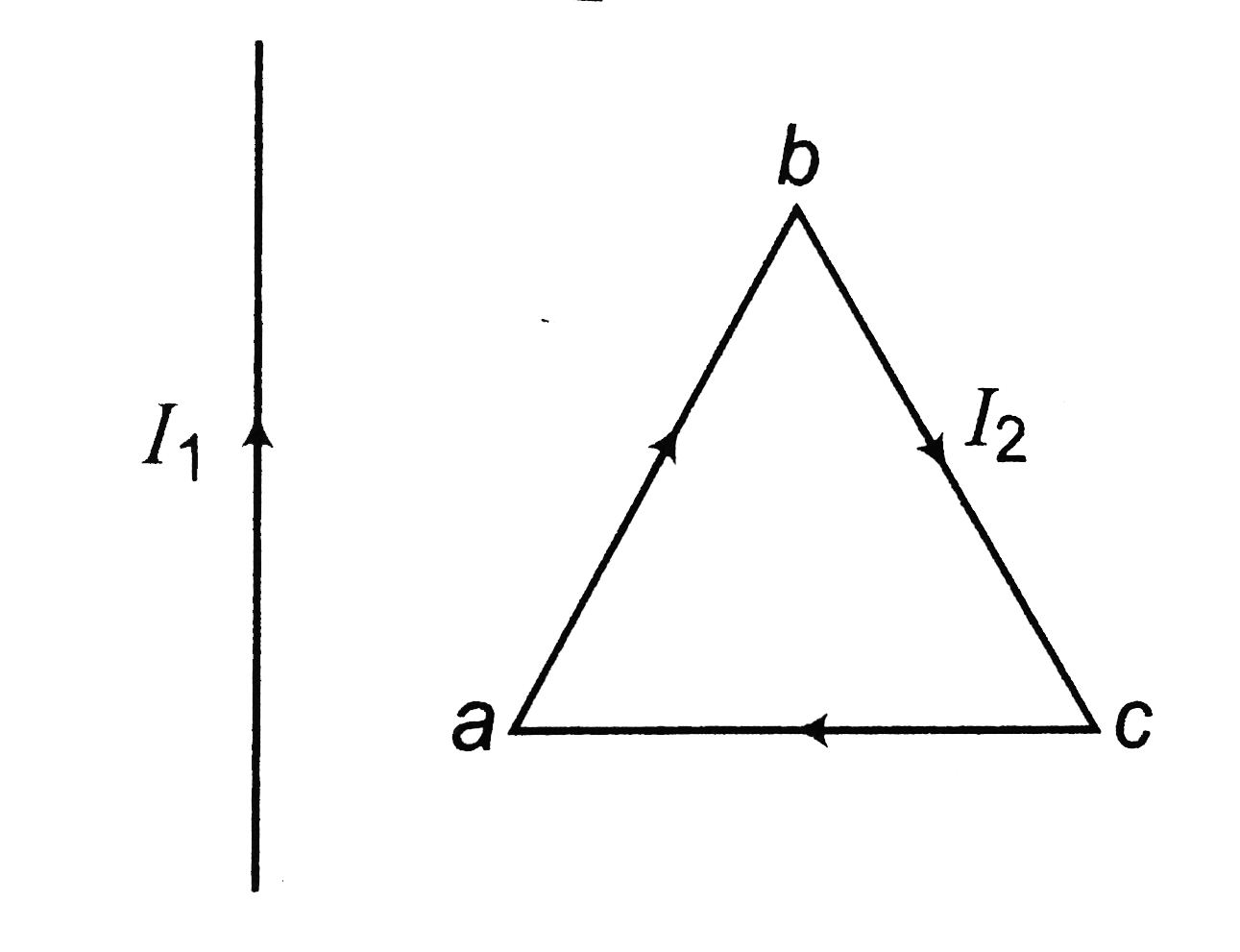
View SolutionThe magnetic field midway between two parallel current carrying wires, carrying currents I and 2i in same direction is B. If the current in the wire with current I is switched off, the magnetic field will become
View SolutionIf current in two parallel wires flow in opposite directions, the force between the wires will:
View SolutionTwo infinitely long straight parallel wires carry equal currents 'I' in the same direction and are 2 m apart. Magnetic induction at a point which is at same normal distance (√2)m from each wire has magnitude
View SolutionTwo thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
View SolutionTwo parallel wires carry equal currents of 10A along the same direction and are separated by a distance of 2.0 cm. Find the magnetic field at a point which is 2.0 cm away from each of these wires.
View SolutionA wire of length L, mass m and carrying a current I is suspended from point O as shown, An another infinitely long wire carrying the same current I is at a distance L below the lower end of the wire. Given i=2A, L=1m and m=0.1kg (In 2=0.693)
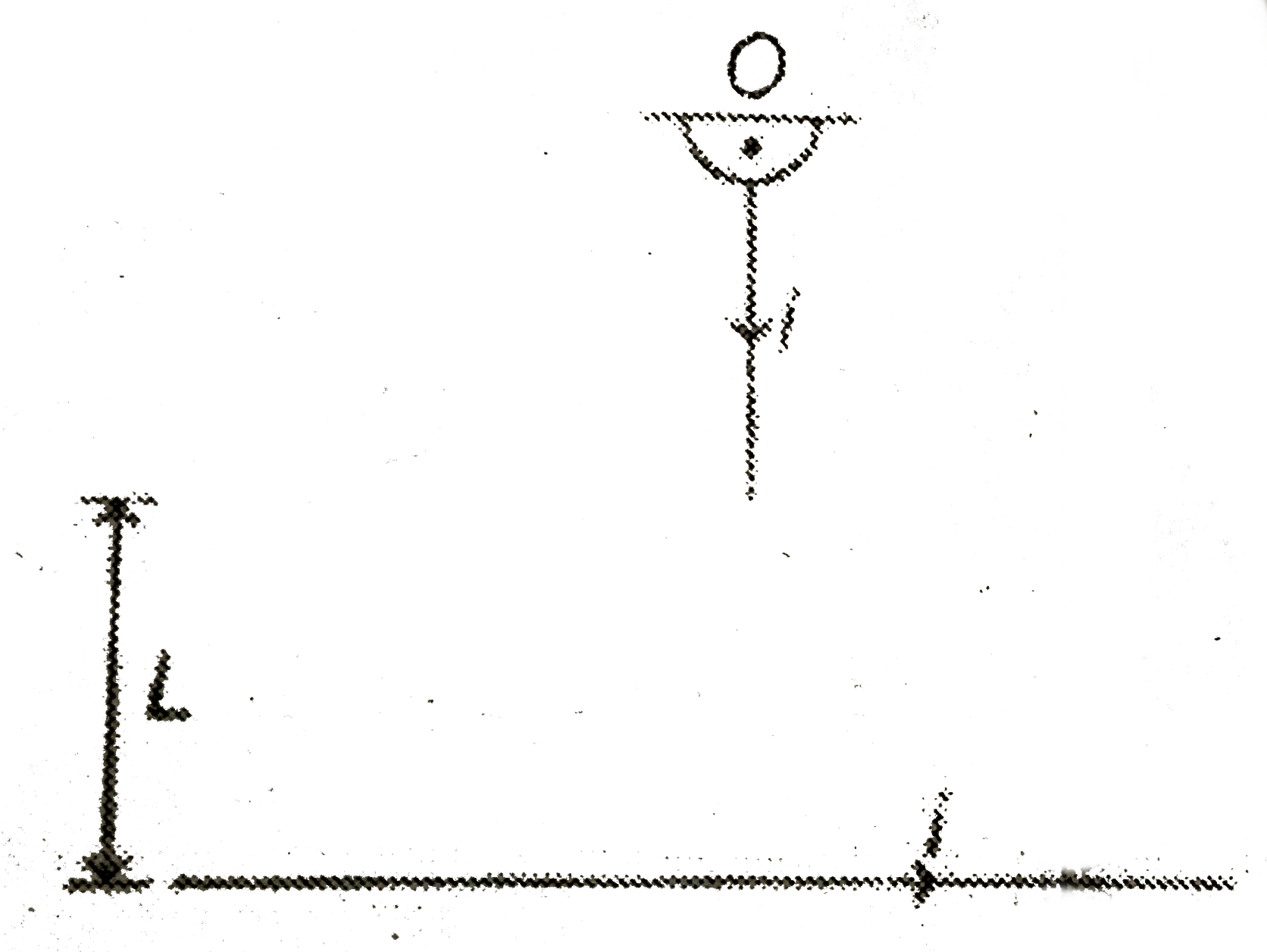
What want to keep the suspended wire stationary by palcing a third inifinitely long wire carrying an upward current. Then this wire should be placed
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionLet two long parallel wires, a distance d apart, carry equal currents I in the same direction. One wires at x=0, the other at x=d (as shown in Fig) Determine magnetic field at any point x-axis between the wires as a function of x.

View Solution