If a charge q is placed at each vertex of a regular polygon, the net electric field at its centre is zero. Show it.

The distance of the centre of a regualr polygon from each vertex will be same. Therefore,
∣∣∣−→E1∣∣∣=∣∣∣−→E2∣∣∣=∣∣∣−→E3∣∣∣ in (a)
∣∣∣−→E1∣∣∣=∣∣∣−→E2∣∣∣=∣∣∣−→E3∣∣∣=∣∣∣−→E4∣∣∣ in (b)
and ∣∣∣−→E1∣∣∣=∣∣∣−→E2∣∣∣=∣∣∣−→E3∣∣∣=∣∣∣−→E4∣∣∣=∣∣∣−→E5∣∣∣ in ( c )
The angle between any two consecutive field vectors for each of a polygon is also same.
Hence, −→E1+−→E2+−→E3+......+−→En=→0
where n = 3, 4, 5, 6..............
Note : →E1+→E2+............+→En⇔→E1+→E2+............+→En−1=−→En
Hence, if a charge q is placed at each vertex except one vertex of regular polygon, then the net electric field at its centre, distant r from each vertex is 14πε0qr2, directed towards or away from the empty vertex depending on whether q is positive or negative.
Similar Questions
Five equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is

View SolutionA charge Q is place at each of the opposite corners of a square. A charge q is placed at each of the other two corners. If the net electrical force on Q is zero, then Q/q equals:
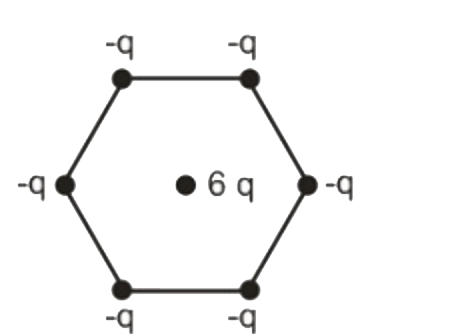
View SolutionSix negative equal charge are placed at the vertical of a regular hexagon . 6q charge is placed at the centre of the hexagon . Find the electric dipole moment of the system.
View SolutionA point charge +Q is placed at the centroid of an equilateral triangle. When a second charge +Q is placed at a vertex of the triangle, the magnitude of the electrostatic force on the central charge is 8 N. The magnitude of the net force on the central charge when a third charge +Q is placed at another vertex of the triangle is
View SolutionA charge Q is placed at each corner of a cube of side a. The potential at the centre of the cube is
View SolutionSix point charges are placed at the vertices of a hexagon of side 1 m as shown in figure. Net electric field at the centre of the hexagon is
View SolutionAssertion : Five charges +q each are placed at five vertices of a regular pentagon. A sixth xharge −Q is placed at the centre of pentagon. Then, net electrostatic force on −Q is zero.
Reason : Net electrostatic potential at the centre is zero.
View SolutionFigure below show regular hexagons with charges at the vertices. In which of the following cases the electric field at the centre is not zero
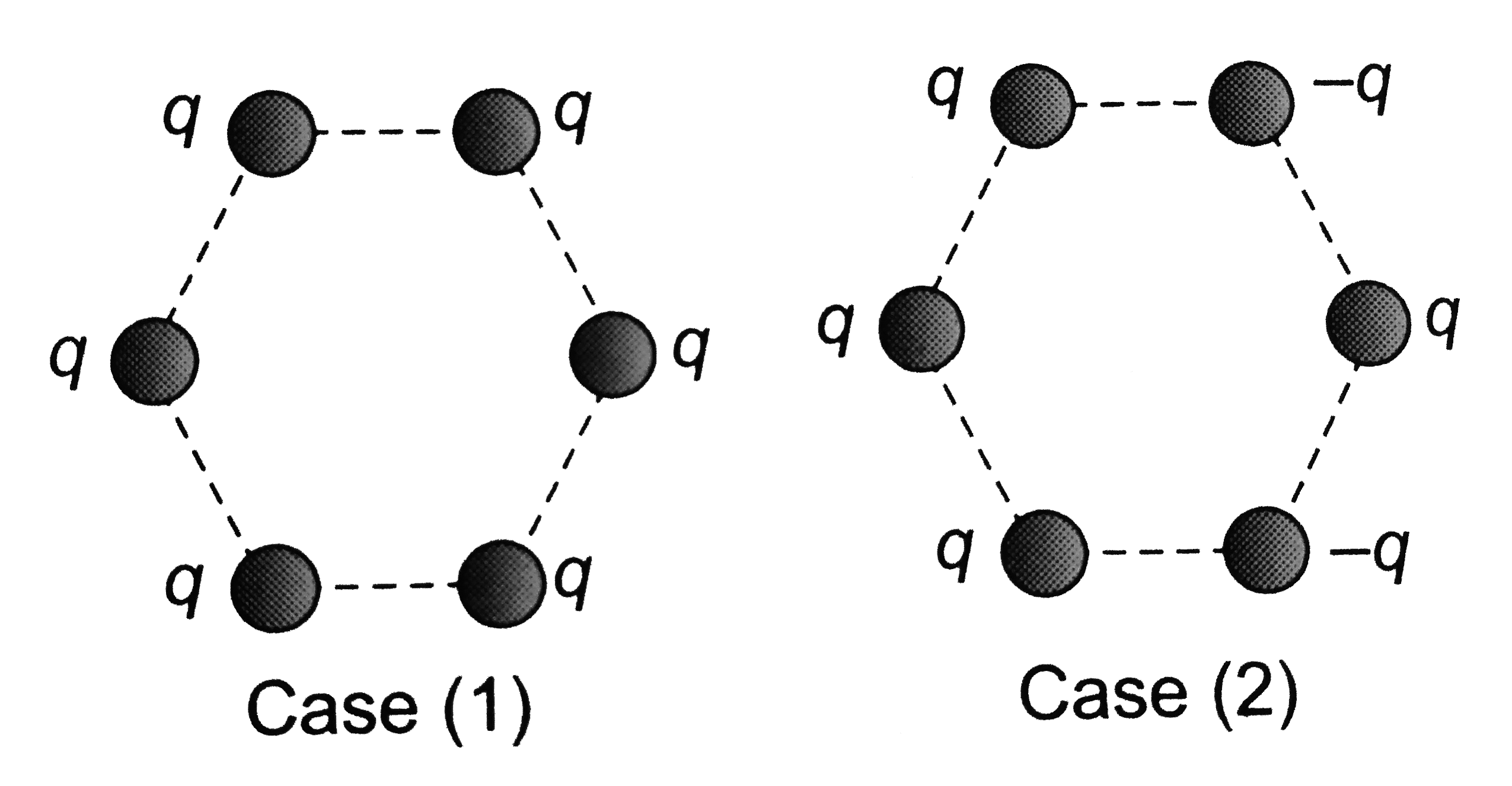
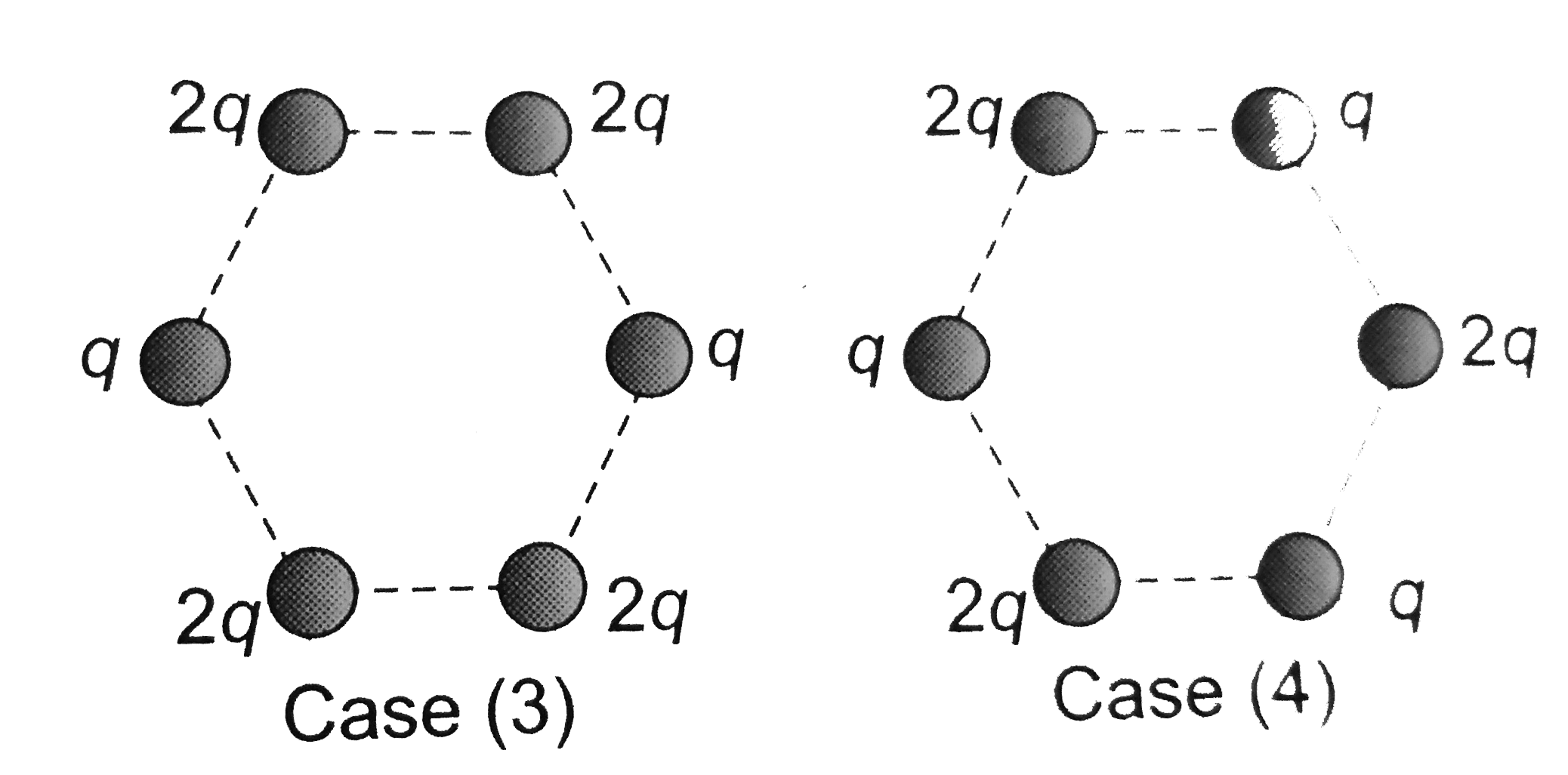
View SolutionFour particles each having a charge q, are placed on the four vertices of a regular pentagon. The distance of each corner from the centre is a. Find the electric field at the centre of the pentagon.
View SolutionFour particles each having a charge q are placed on the four vertices of a regular pentagon. The distance of each corner from the centre is 'a'. Find the electric field at the centre of pentagon.
View Solution
