The displacement s of an object is given as a function of time t by the following equation s=2t+5t2+3t3. Calculate the instantaneous velocity of the object at t = 1 s.
The correct Answer is:21m/s
v=dsdt
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISE
29 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - A)
58 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
Similar Questions
The displacement s of an object is given as a function of time t
s=5t2+9t
Calculate the instantaneous velocity of object at t = 0.
View SolutionThe displacement x of an object is given as a function of time x=2t+3t2
Calculate the instantaneous velocity of the object at t = 2 s
View SolutionThe velocity of an object is changing with time and relation is given by the following equation.
v=2t+3t2
Calculate the position of the object from the origin at t = 2 s.
Assume particle to be at origin at t = 0
View SolutionThe displacement x of an object is given as a funstion of time, x=2t+3t2. The instantaneous velocity of the object at t = 2 s is
View SolutionThe displacement (in metre) of a particle moving along x-axis is given by x=18t+5t2. Calculate (i) the instantaneous velocity t=2s (ii) average velocity between t=2s to t=3s (iii) instantaneous acceleration.
View SolutionA particle starts from origin with uniform acceleration. Its displacement after t seconds is given in meter by the relation x=2+5t+7t2. Calculate the magnitude of its
a. Initial velocity
b. Velocity at t=4s
c. Uniform acceleration
d. Displacement at t=5s
View SolutionThe velocity of an object moving rectilinearly is given as a function of time by v=4t−3t2 where v is in m/s and t is in seconds. The average velocity if particle between t=0 to t=2 seconds is
View SolutionA particle is moving on a straight line with velocity (v) as a function of time (t) according to relation v=(5t2−3t+2)m/s . Now give the answer of following questions :
Velocity of particle at t = 3 sec. is :
View SolutionIn the s−t equations (s=10+20t−5t2) match the following
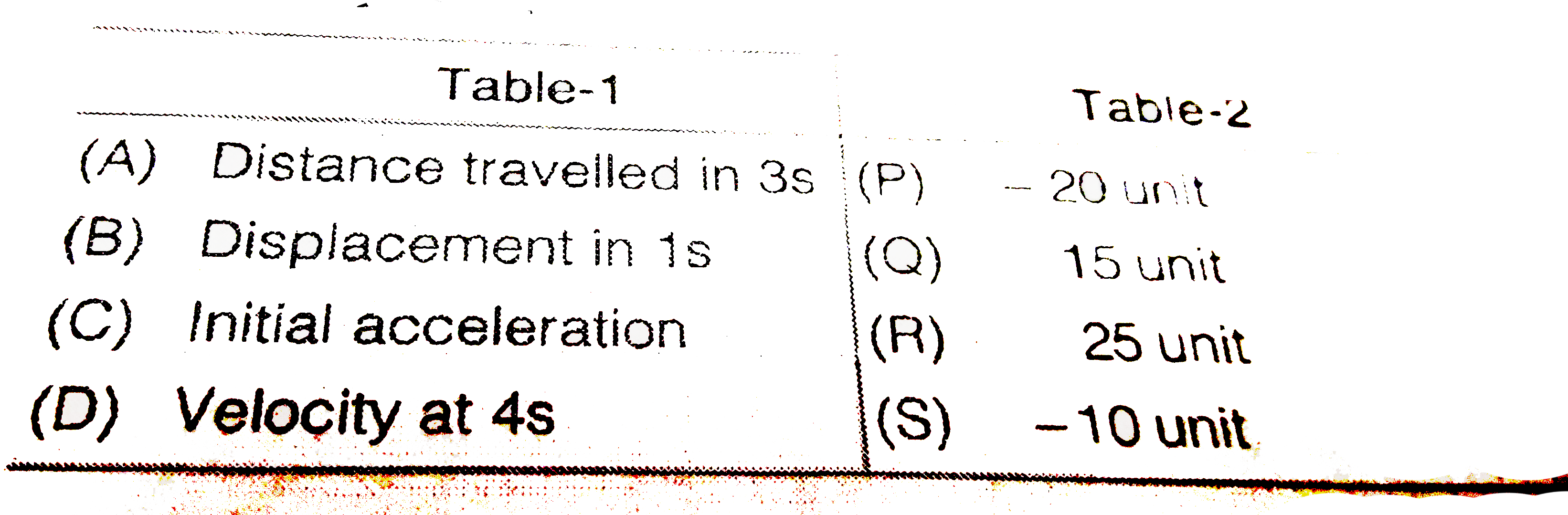
View SolutionThe displacement of an object of mass 3 kg is given by the relation S=13t2, where t is time in seconds. If the work done by the net force on the object in 2 s is pq joule, where p and q are smallest integer values, then what is the value of p+q?
View Solution
