A capacitor of capacitance C, charged to a potential difference V, is discharged through a series combination of two resistors R1 and R2. Find the heat generated in resistor R1 during discharging.
To find the heat generated in resistor R1 during the discharging of a capacitor through a series combination of two resistors R1 and R2, we can follow these steps:
Step 1: Determine the maximum energy stored in the capacitor
The maximum energy U stored in a capacitor is given by the formula:
U=12CV2
where C is the capacitance and V is the potential difference across the capacitor.
Step 2: Understand the energy distribution in the resistors
When the capacitor discharges through the resistors R1 and R2, the total energy stored in the capacitor is converted into heat energy in the resistors. Therefore, the total heat generated in both resistors is equal to the energy stored in the capacitor:
Qtotal=U=12CV2
Step 3: Apply the formula for heat generated in resistors
The heat generated in each resistor can be expressed using Joule's law:
Q1=I2R1andQ2=I2R2
where I is the current flowing through the circuit. Since the resistors are in series, the same current flows through both.
Step 4: Relate the heat generated to the total energy
The total heat generated in both resistors can be expressed as:
Qtotal=Q1+Q2=I2R1+I2R2
This can be factored as:
Qtotal=I2(R1+R2)
Step 5: Equate the total heat to the energy stored in the capacitor
From the previous steps, we have:
I2(R1+R2)=12CV2
From this, we can solve for the current I:
I2=12CV2R1+R2
Step 6: Find the heat generated in resistor R1
Now, substituting I2 back into the equation for heat generated in R1:
Q1=I2R1=⎛⎝12CV2R1+R2⎞⎠R1
This simplifies to:
Q1=CV2R12(R1+R2)
Final Result
Thus, the heat generated in resistor R1 during the discharging of the capacitor is:
Q1=CV2R12(R1+R2)
The maximum energy U stored in a capacitor is given by the formula:
U=12CV2
where C is the capacitance and V is the potential difference across the capacitor.
When the capacitor discharges through the resistors R1 and R2, the total energy stored in the capacitor is converted into heat energy in the resistors. Therefore, the total heat generated in both resistors is equal to the energy stored in the capacitor:
Qtotal=U=12CV2
The heat generated in each resistor can be expressed using Joule's law:
Q1=I2R1andQ2=I2R2
where I is the current flowing through the circuit. Since the resistors are in series, the same current flows through both.
The total heat generated in both resistors can be expressed as:
Qtotal=Q1+Q2=I2R1+I2R2
This can be factored as:
Qtotal=I2(R1+R2)
From the previous steps, we have:
I2(R1+R2)=12CV2
From this, we can solve for the current I:
I2=12CV2R1+R2
Now, substituting I2 back into the equation for heat generated in R1:
Q1=I2R1=⎛⎝12CV2R1+R2⎞⎠R1
This simplifies to:
Q1=CV2R12(R1+R2)
Thus, the heat generated in resistor R1 during the discharging of the capacitor is:
Q1=CV2R12(R1+R2)
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-J
10 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-H ( MULTIPLE TRUE-FALE TYPE QUESTIONS)
5 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
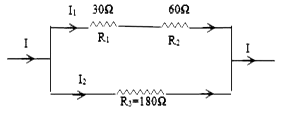
In Figure below, power developed in resistor R1 is 120W. Find the power developed in resistor R3.
View SolutionA capacitance C charged to a potential difference V is discharged by connecting its plates through a resistance R. Find the heat dissipated in one time constant after the connections are made. Do this by calculating ∫i2Rdtand also by finding the decrease in the energy stored in the capacitor.
View SolutionA capacitor is charged to a certain potential and then allowed to discharge through a resistance R. The ratio of charge on the capacitor to current in the circuit
View SolutionA capacitor of capacitance 2μF is charged to a potential difference of 5V. Now, the charging battery is disconected and the capacitor is connected in parallel to a resistor of 5Ω and another unknown resistor of resistance R as shown in figure. If the total heat produced in 5Ω resistance is 10μJ then the unknown resistance R is equal to
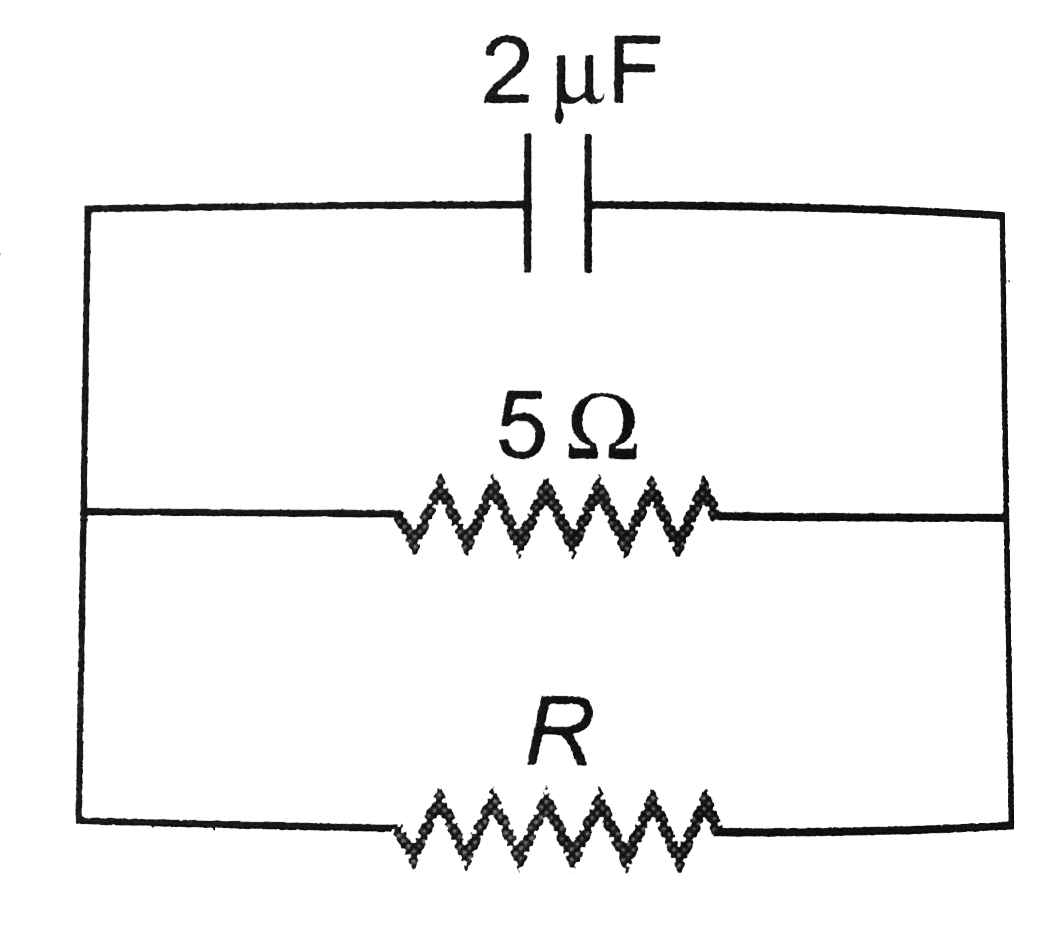
View SolutionA capacitor of capacitance 2μF is charged to a potential difference of 5V. Now, the charging battery is disconected and the capacitor is connected in parallel to a resistor of 5Ω and another unknown resistor of resistance R as shown in figure. If the total heat produced in 5Ω resistance is 10μJ then the unknown resistance R is equal to

View SolutionTwo identical capacitors A and B are charged to the same potential and then made to discharge through resistances RA and RB respectively, with RA>RB.
View SolutionA capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
View SolutionA capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View SolutionFind the current through resistor R
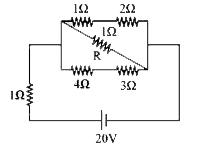
View SolutionFind the currents going through the three resistors R1,R2 and R3 in the circuit of figure.

View Solution
