The figure shows an infinite circuit formed by the repetiton of the same link , consisting of resistance R1=4.0Ω and R2=3.0Ω . Find the resisance of this circuit between points A and B.
To find the equivalent resistance RAB of the infinite circuit formed by the resistors R1=4.0Ω and R2=3.0Ω between points A and B, we can follow these steps:
Step 1: Define the Equivalent Resistance
Let the equivalent resistance between points A and B be denoted as RAB=x.
Step 2: Analyze the Circuit
In the given infinite circuit, the first resistor R1 is connected in series with the equivalent resistance of the rest of the circuit (which is also x). The second resistor R2 is connected in parallel with this combination.
Step 3: Set Up the Equation
Using the rules for series and parallel resistances, we can express the relationship as follows:
1x=1R1+Rparallel
Where Rparallel is the equivalent resistance of R2 in parallel with x.
The equivalent resistance of R2 and x in parallel can be expressed as:
Rparallel=R2⋅xR2+x
Substituting R1 and R2:
Rparallel=3.0⋅x3.0+x
Step 4: Substitute and Rearrange
Now substituting Rparallel into the equation for x:
1x=14.0+3.0⋅x3.0+x
Step 5: Cross Multiply
Cross multiplying gives:
1=x⎛⎝14.0+3.0⋅x3.0+x⎞⎠
Step 6: Simplify the Equation
This leads to:
1=x(3.0+x)4.0(3.0+x)+3.0x
Expanding and simplifying:
1=x(3.0+x)12.0+4.0x+3.0x
1=x(3.0+x)12.0+7.0x
Step 7: Cross Multiply Again
Cross multiplying gives:
12.0+7.0x=x(3.0+x)
Expanding:
12.0+7.0x=3.0x+x2
Step 8: Rearranging to Form a Quadratic Equation
Rearranging gives:
x2−4.0x−12.0=0
Step 9: Solve the Quadratic Equation
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=1,b=−4,c=−12:
x=4±√(−4)2−4⋅1⋅(−12)2⋅1
x=4±√16+482
x=4±√642
x=4±82
Step 10: Calculate the Values
Calculating the two possible values:
1. x=122=6Ω
2. x=−42=−2Ω (not physically meaningful)
Thus, the equivalent resistance RAB is:
RAB=6Ω
Final Answer
The resistance of the circuit between points A and B is 6Ω.
---
Let the equivalent resistance between points A and B be denoted as RAB=x.
In the given infinite circuit, the first resistor R1 is connected in series with the equivalent resistance of the rest of the circuit (which is also x). The second resistor R2 is connected in parallel with this combination.
Using the rules for series and parallel resistances, we can express the relationship as follows:
1x=1R1+Rparallel
Where Rparallel is the equivalent resistance of R2 in parallel with x.
Rparallel=R2⋅xR2+x
Substituting R1 and R2:
Rparallel=3.0⋅x3.0+x
Now substituting Rparallel into the equation for x:
1x=14.0+3.0⋅x3.0+x
Cross multiplying gives:
1=x⎛⎝14.0+3.0⋅x3.0+x⎞⎠
This leads to:
1=x(3.0+x)4.0(3.0+x)+3.0x
Expanding and simplifying:
1=x(3.0+x)12.0+4.0x+3.0x
1=x(3.0+x)12.0+7.0x
Cross multiplying gives:
12.0+7.0x=x(3.0+x)
Expanding:
12.0+7.0x=3.0x+x2
Rearranging gives:
x2−4.0x−12.0=0
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=1,b=−4,c=−12:
x=4±√(−4)2−4⋅1⋅(−12)2⋅1
x=4±√16+482
x=4±√642
x=4±82
Calculating the two possible values:
1. x=122=6Ω
2. x=−42=−2Ω (not physically meaningful)
RAB=6Ω
The resistance of the circuit between points A and B is 6Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:AAKASH INSTITUTE ENGLISHChapter:CURRENT ELECTRICITYExercise:Try Yourself
Explore 34 Videos
- CURRENT ELECTRICITYBook:AAKASH INSTITUTE ENGLISHChapter:CURRENT ELECTRICITYExercise:ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))
Explore 69 Videos
- COMMUNICATION SYSTEMS Book:AAKASH INSTITUTE ENGLISHChapter:COMMUNICATION SYSTEMS Exercise:ASSIGNMENT SECTION D (Assertion-Reason)
Explore 10 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
Similar Questions
In the circuit shown in Fig. the emf of the sources is equal to ξ=5.0V and the resistances are equal to R1=4.0Ω and R2=6.0Ω. The internal resistance of the source equals R=1.10Ω. Find the currents flowing through the resistances R1 and R2.
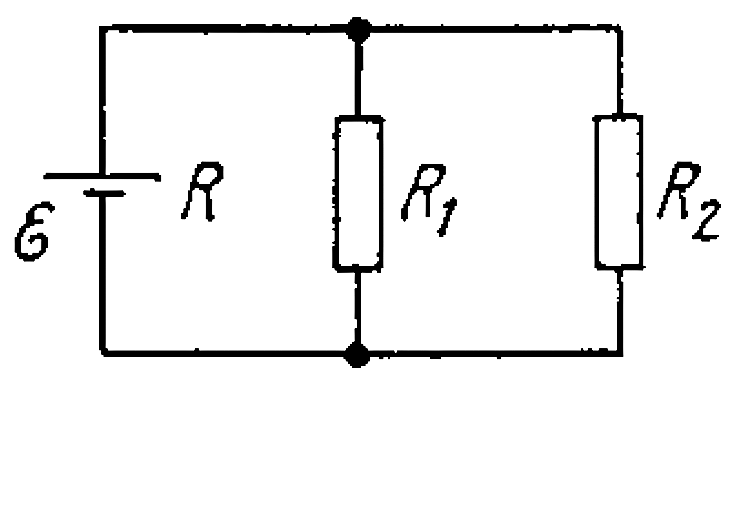
View Solution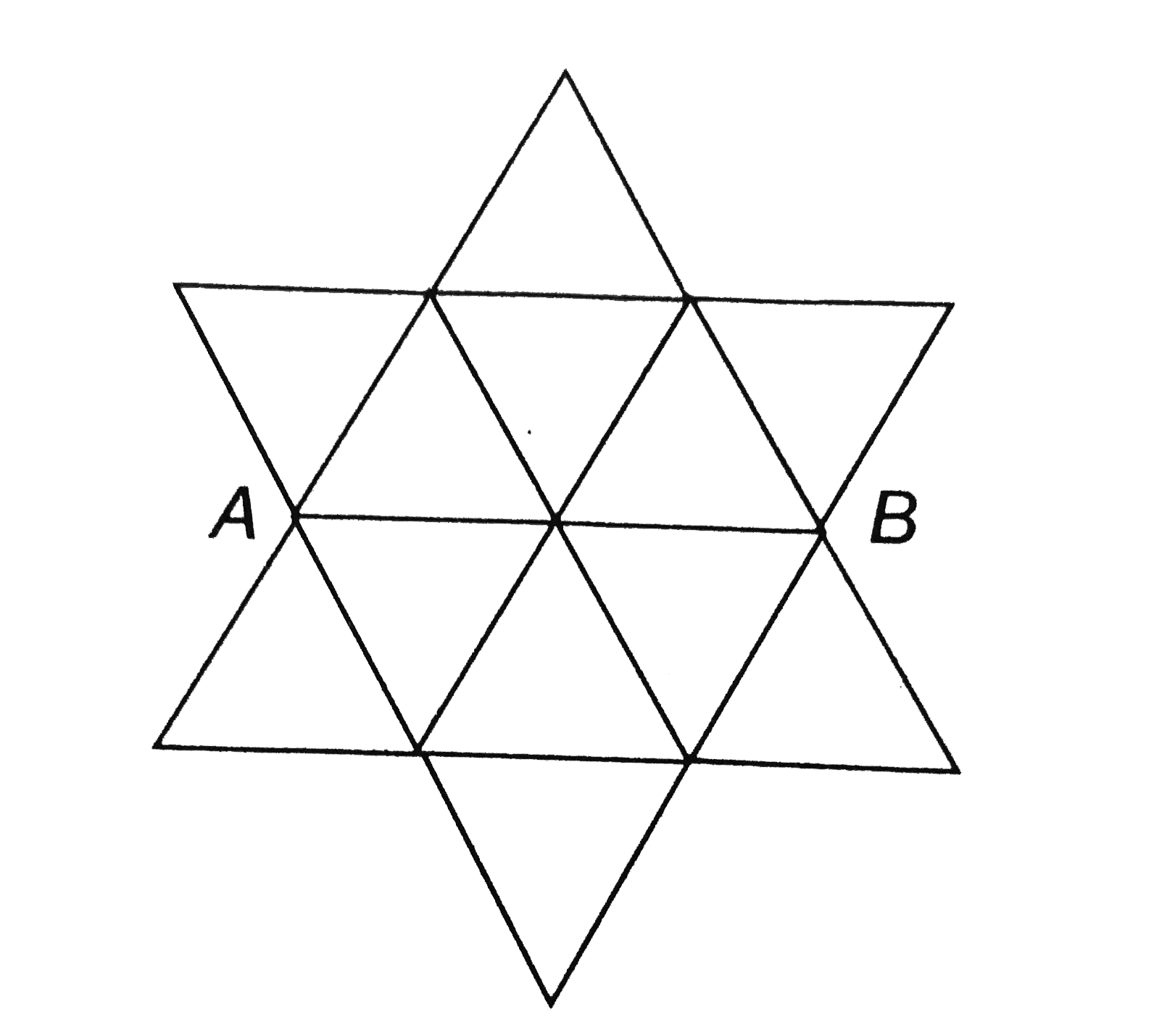
If the resistance of each branch of the circuit shown below is 1Ω , then the equivalent resistance of the circuit between the points A and B is
View Solution
Knowledge Check
Two resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
A(66.7±1.8)ΩB(66.7±4.0)ΩC(66.7±3.0)ΩD(66.7±7.0)Ω
Two resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
View SolutionIn a series R, L, C circuit XL=10Ω,Xc=4ωand R=6Ω. Find the power factor of the circuit
View SolutionTwo resistor of resistance R1=(6±0.09)Ω and R2=(3±0.09)Ω are connected in parallel the equivalent resistance R with error (in Ω)
View SolutionTwo resistor R1=(24±0.5)ΩandR2=(8±0.3)Ωare joined in series, The equivalent resistence is
View SolutionFind the current flowing through the resistance R1 of the circuit shown in Fig. If the resistances are equal to R1=10Ω.R2=20Ω and R3=30Ω, and the potential of points 1,2 and 3 are equal to φ1=10V,φ2=6V, and φ3=5V

View SolutionThe circuit consists of two resistors (of resistance R1=20Ω and R2=10Ω), a capacitor (of capacitance C=10μF) and two ideal cells. In the circuit shown the capacitor is in steady state and the switch S is open

The current through the resistor R2 just after the switch S is closed is :
View SolutionThe circuit consists of two resistors (of resistance R1=20Ω and R2=10Ω), a capacitor (of capacitance C=10μF) and two ideal cells. In the circuit shown the capacitor is in steady state and the switch S is open
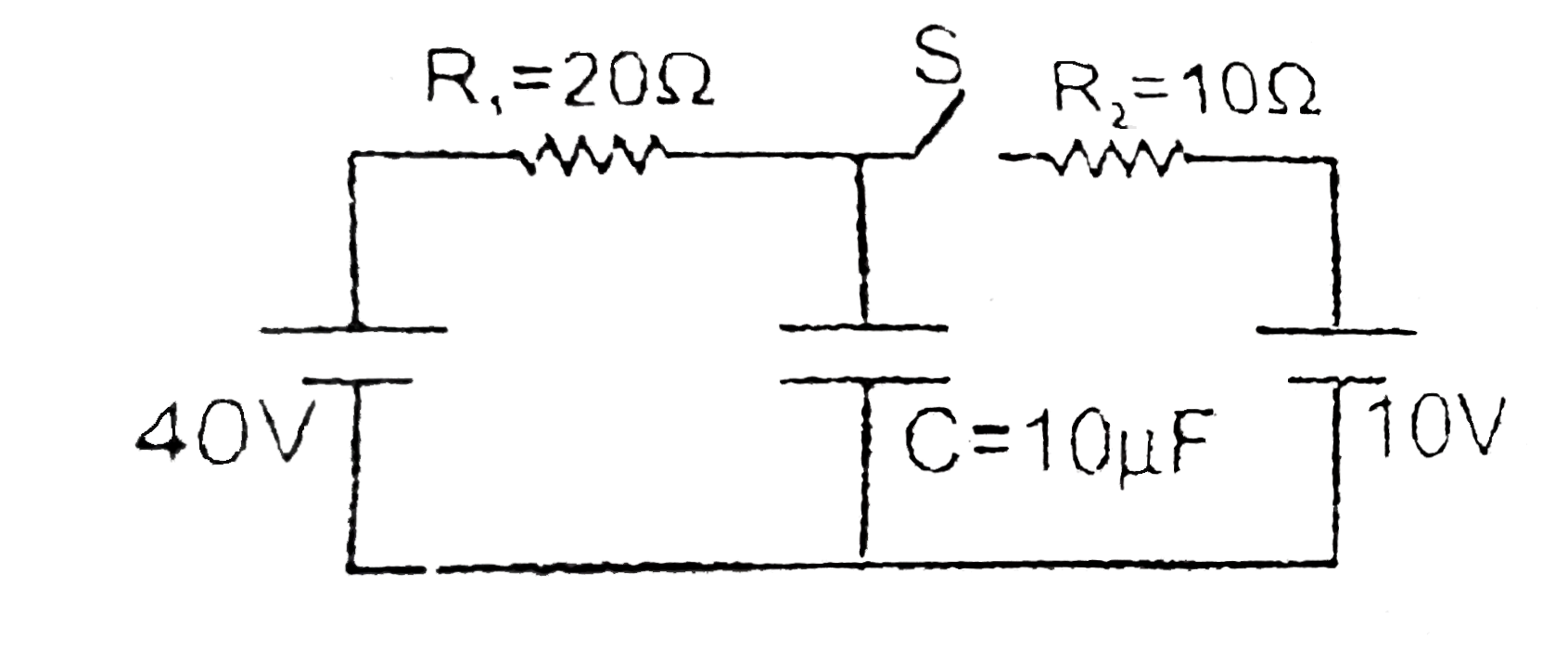
The charge on capacitor in steady state with switch S closed.
View Solution