Charge through a cross-section of a conductor is given by Q=(2t2+5t)C. Find the current through the conductor at the instant t=2s.
Charge Q=(2t2+5t)C
Instantaneous current I=dQdt=ddt(2t2+5t)
At t=2s,l=(4×2)+5=13A
Related Playlists
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Try Yourself34videos
CURRENT ELECTRICITY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))69videos
CURRENT ELECTRICITY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)10videos
COMMUNICATION SYSTEMS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)10videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
Charge through a cross-section of a conductor is given by Q = (2t2+5t)C Find the current through the conductor at the instant t = 2s.
View SolutionCharge through a cross-section of a conductor is given by Q=5t2−2t coulomb . Find the average current through the conductor in the interval t1=2s to t2=4s
(1) 14s (2) 28 A
(3) 56A (4) 7AView SolutionCharge through a cross section of a conductor is give by Q=5t2−2t coulomb .Find the average current through the conduction the interval t1=2s to t2=4s .
View SolutionIf charge through a cross-section of a conductor at timetis q=2t2+3t+1. Find the current at t = 2s.
View SolutionCharge Q passing through a cross-section of conductor at an instant is given by Q=(0.5t2+t)C where t is in second . Current through the conductor at t=1 is
View SolutionA charge 0.5C passes through a cross section of a conductor in 5s. Find the current.
View SolutionThe current through an inductor of 1H is given by i=3tsint. Find the voltage across the inductor.
View SolutionIn th circuit the key (K) is closed at t=0. Find the current in ampere through the key (K) at the instant t=102ln2 sec.
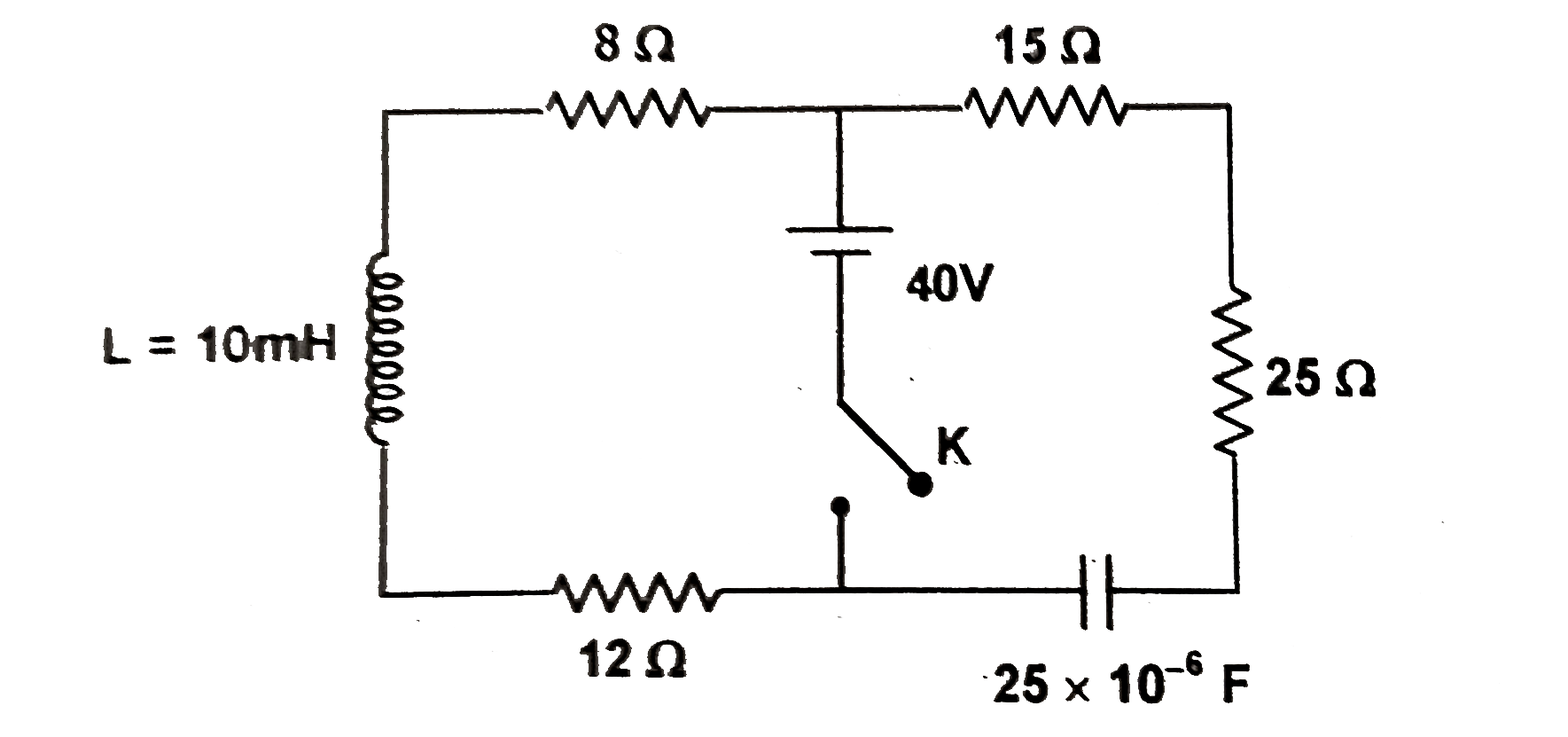 View Solution
View SolutionIf n,e,A and vd are free electron density inside conductor , charge of electron , area of cross-section of conductor and drift velocity of free electrons inside conductor, then current l through the conductor is
View SolutionIn the circuit shown the key (K) is closed at t=0, the current through the key at the instant t=10−3ln,2 is
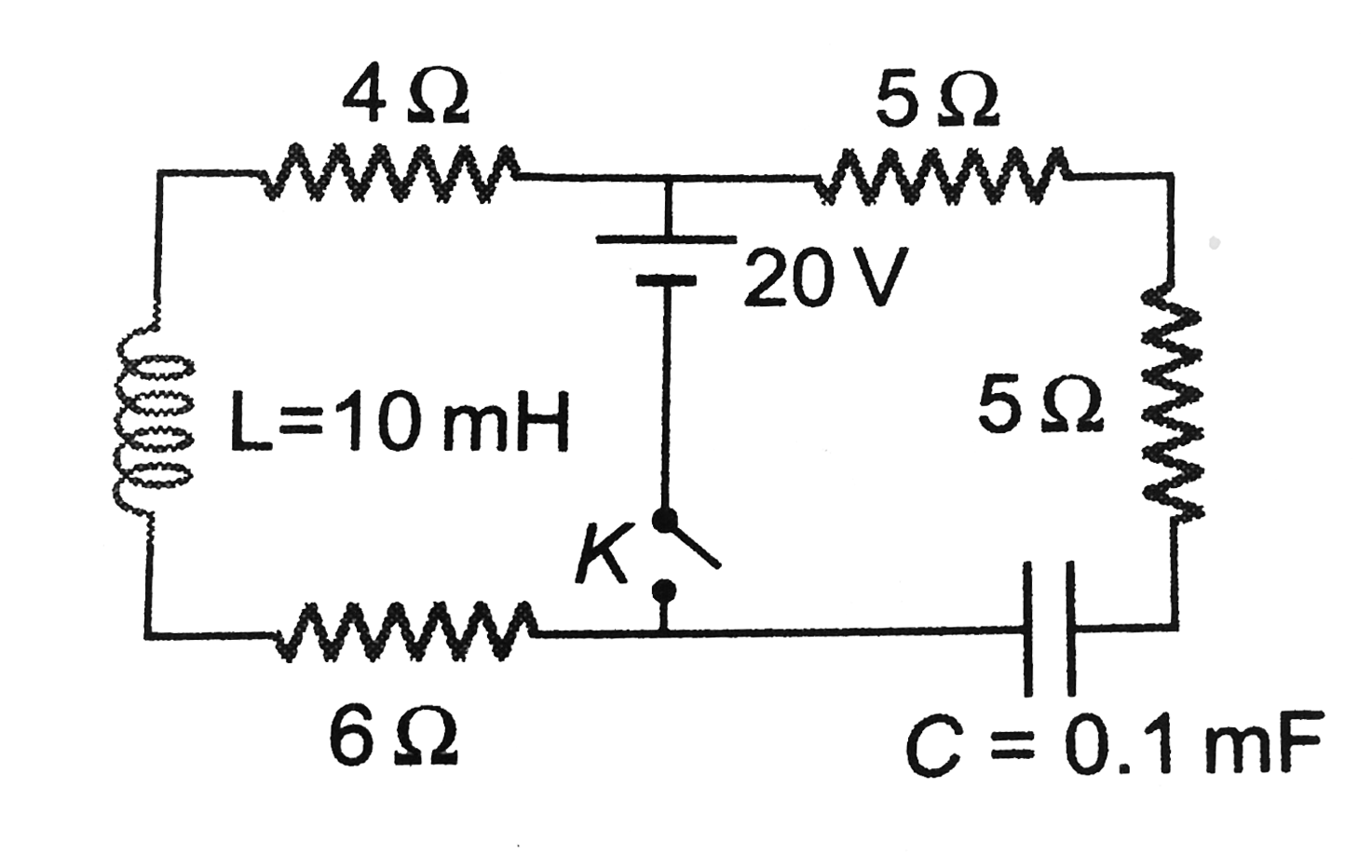 View Solution
View Solution


