106 positrons are flowing normally through an area in forward direction and same amount of electrons are flowing in backward direction in the interval of 10 ms.Find the current through the area.
To find the current through the area where 10^6 positrons are flowing in one direction and the same number of electrons are flowing in the opposite direction over an interval of 10 ms, we can follow these steps:
Step 1: Understand the charges involved
- Positrons have a charge of +1.6 x 10^-19 C (the same magnitude as the electron's charge but positive).
- Electrons have a charge of -1.6 x 10^-19 C.
Step 2: Calculate the total charge flowing
Since there are 10^6 positrons and 10^6 electrons, the total charge contributed by each type of particle can be calculated as follows:
- Charge due to positrons:
Qpositrons=npositrons×e=106×1.6×10−19C
- Charge due to electrons:
Qelectrons=nelectrons×e=106×1.6×10−19C
Step 3: Calculate the total charge
Since both charges are equal in magnitude but opposite in direction, the effective charge contributing to the current will be the sum of the absolute values of the charges:
Qtotal=Qpositrons+|Qelectrons|=106×1.6×10−19+106×1.6×10−19
Qtotal=2×(106×1.6×10−19)=3.2×10−13C
Step 4: Convert time to seconds
The time interval given is 10 ms, which needs to be converted to seconds:
t=10ms=10×10−3s=10−2s
Step 5: Calculate the current
Current (I) is defined as the charge (Q) flowing per unit time (t):
I=Qtotalt
Substituting the values we found:
I=3.2×10−13C10−2s=3.2×10−11A
Final Answer
The total current through the area is:
I=3.2×10−11A
- Positrons have a charge of +1.6 x 10^-19 C (the same magnitude as the electron's charge but positive).
- Electrons have a charge of -1.6 x 10^-19 C.
Since there are 10^6 positrons and 10^6 electrons, the total charge contributed by each type of particle can be calculated as follows:
Qpositrons=npositrons×e=106×1.6×10−19C
Qelectrons=nelectrons×e=106×1.6×10−19C
Since both charges are equal in magnitude but opposite in direction, the effective charge contributing to the current will be the sum of the absolute values of the charges:
Qtotal=2×(106×1.6×10−19)=3.2×10−13C
The time interval given is 10 ms, which needs to be converted to seconds:
t=10ms=10×10−3s=10−2s
Current (I) is defined as the charge (Q) flowing per unit time (t):
I=Qtotalt
Substituting the values we found:
I=3.2×10−13C10−2s=3.2×10−11A
The total current through the area is:
I=3.2×10−11A
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Try Yourself
34 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))
69 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Knowledge Check
The direction of the flow of current through electric circuit is
Afrom low potential to high potential.Bfrom high potential to low potential.Cdoes not depend upon potential valueDcurrent cannot flow through circuit.
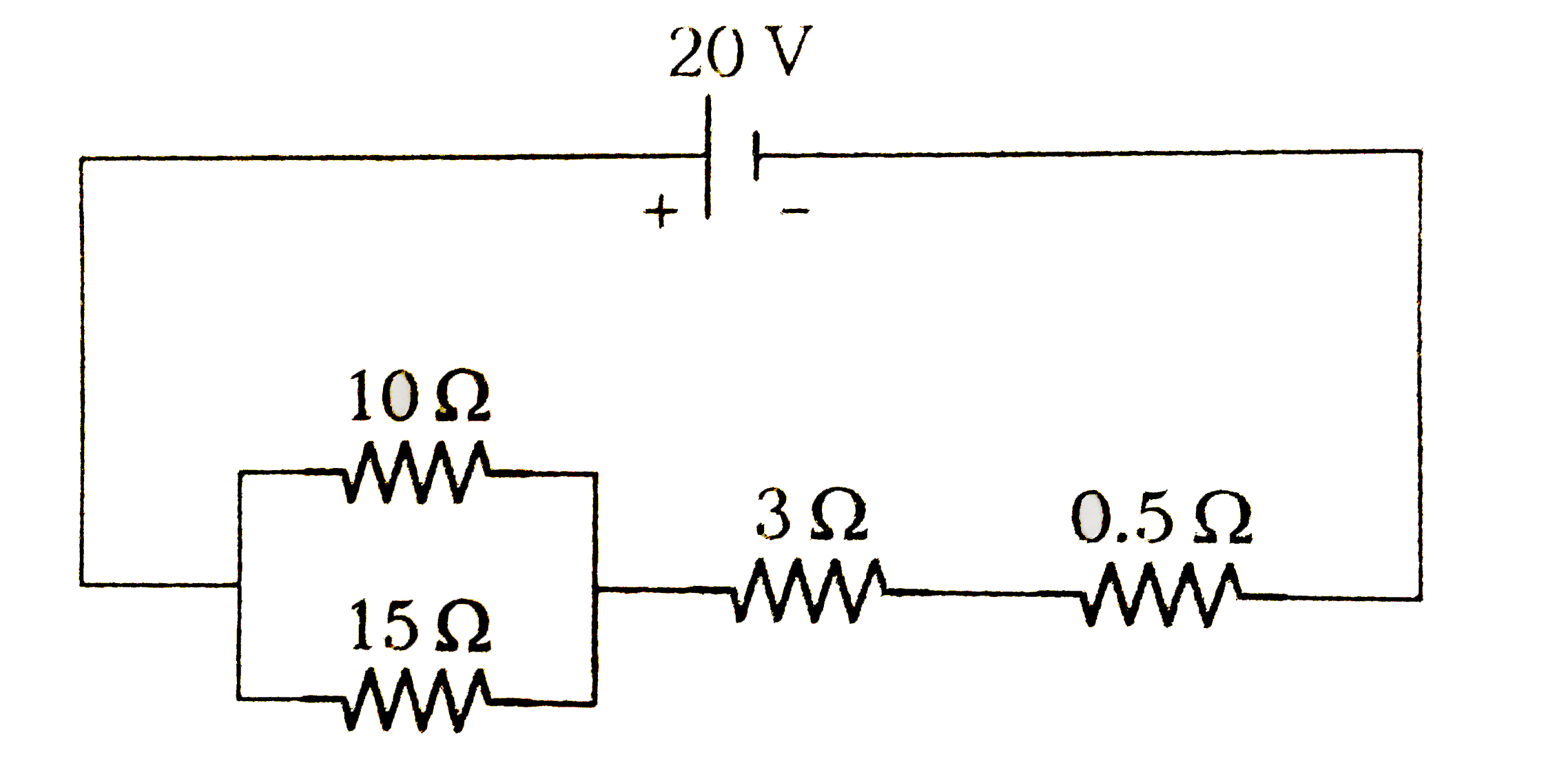
In the circuit, the current flowing through 10Ω resistance is
View SolutionIn a gas discharge tube, if 3×1018 electrons are flowing per sec from left to right and 2×1018 protons are flowing per second from right to left of a given cross-section, the magnitude and direction of current through the cross-section :
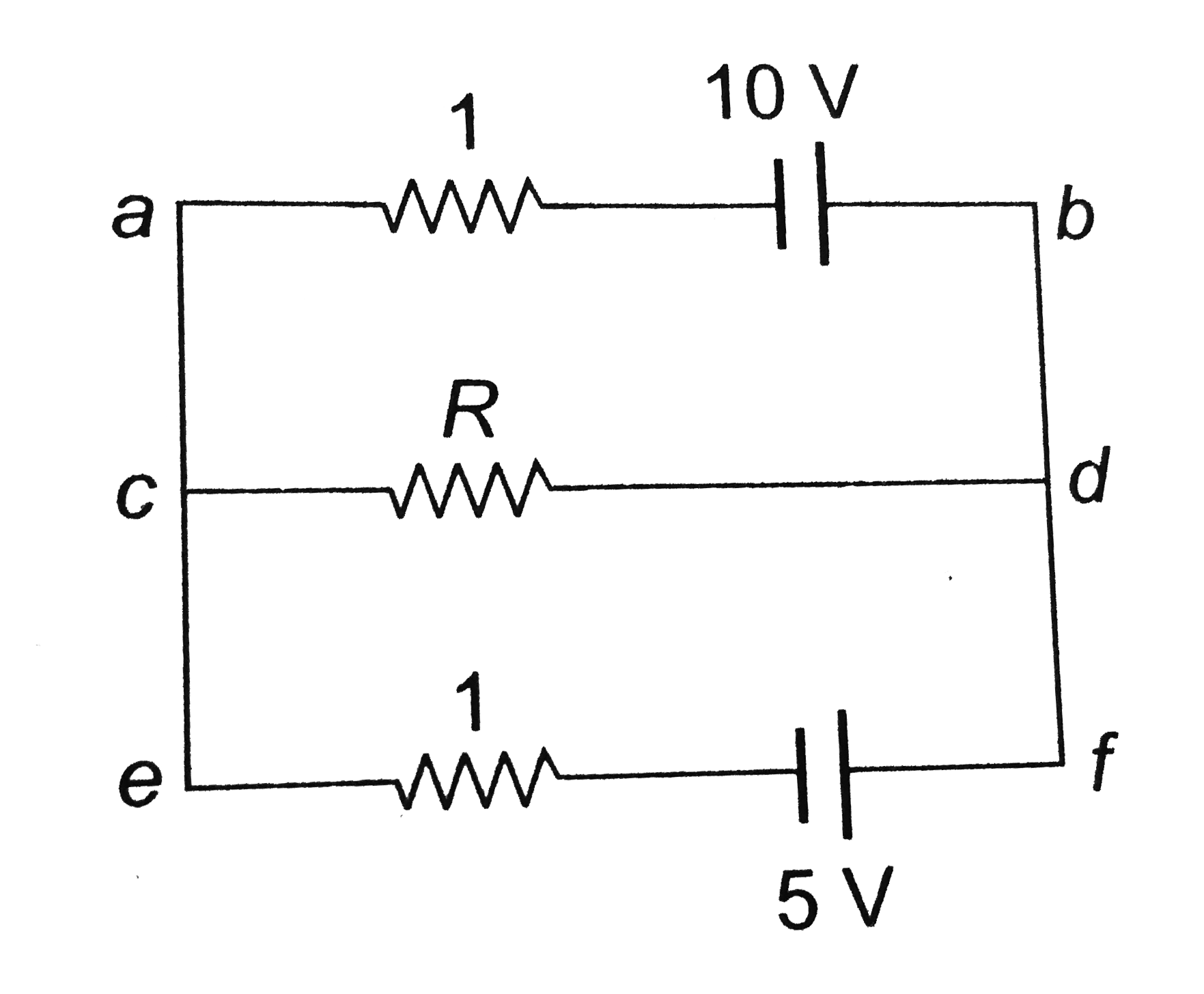
View SolutionFind the value of R for which no current will flow through 5V battery
View SolutionA flow of 107 electrons per second in a conducing wire constitutes a current of .
View SolutionA current of 4.8 A is flowing in a conductor the number of electrons passing per sec through the conductor will be
View Solutionn electrons flow through a cross section of a conductor in time t. If charge on an electron is e, then write an expression for the current in the conductor.
View SolutionIf a current of one ampere flows through a metal wire for one hour, how many electrons would flow through the wire in 2 seconds?
View Solution
