An electric dipole of 100ˆk pC-m is located at origin. Determine the field and potential at point P(1m,π3,π2) in spherical coordinate system p(r,θ,ϕ)
To solve the problem, we need to determine the electric field and potential at point P given the electric dipole moment. Let's break it down step by step.
Step 1: Understand the given information
We have an electric dipole moment p=100^k pC-m located at the origin. The point P is given in spherical coordinates as P(1,π3,π2).
Step 2: Convert the dipole moment to SI units
The dipole moment p in SI units is:
p=100×10−12C-m=1×10−10C-m
Step 3: Identify the coordinates of point P
From the spherical coordinates:
- r=1m
- θ=π3
- ϕ=π2
Step 4: Use the electric field formula for a dipole
The electric field E due to a dipole at a point in space is given by:
E=14πϵ0(3(p⋅^r)^r−pr3)
However, in spherical coordinates, we can use the simplified formula for the electric field of a dipole aligned along the z-axis:
E=kpr3(2cosθ^r+sinθ^θ)
where k=1/(4πϵ0).
Step 5: Substitute values into the electric field formula
Substituting the values:
- k=9×109N m2/C2
- p=1×10−10C-m
- r=1m
- θ=π3
Calculating E:
E=9×109⋅1×10−1013(2cos(π3)^r+sin(π3)^θ)
=9×109⋅10−10(2⋅12^r+√32^θ)
=9×10−1(^r+√32^θ)
=0.9^r+0.9√32^θ
Step 6: Calculate the potential at point P
The potential V due to a dipole is given by:
V=kpcosθr2
Substituting the values:
V=9×109⋅1×10−10⋅cos(π3)12
=9×109⋅10−10⋅12
=920V
Final Results
- The electric field at point P is:
E=0.9^r+0.9√32^θN/C
- The potential at point P is:
V=920V
We have an electric dipole moment p=100^k pC-m located at the origin. The point P is given in spherical coordinates as P(1,π3,π2).
The dipole moment p in SI units is:
p=100×10−12C-m=1×10−10C-m
From the spherical coordinates:
- r=1m
- θ=π3
- ϕ=π2
The electric field E due to a dipole at a point in space is given by:
E=14πϵ0(3(p⋅^r)^r−pr3)
However, in spherical coordinates, we can use the simplified formula for the electric field of a dipole aligned along the z-axis:
E=kpr3(2cosθ^r+sinθ^θ)
where k=1/(4πϵ0).
Substituting the values:
- k=9×109N m2/C2
- p=1×10−10C-m
- r=1m
- θ=π3
E=9×109⋅1×10−1013(2cos(π3)^r+sin(π3)^θ)
=9×109⋅10−10(2⋅12^r+√32^θ)
=9×10−1(^r+√32^θ)
=0.9^r+0.9√32^θ
The potential V due to a dipole is given by:
V=kpcosθr2
Substituting the values:
V=9×109⋅1×10−10⋅cos(π3)12
=9×109⋅10−10⋅12
=920V
- The electric field at point P is:
E=0.9^r+0.9√32^θN/C
- The potential at point P is:
V=920V
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:EXAMPLE
Explore 138 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:EXERCISE
Explore 20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:SECTION-I Subjective Type Questions
Explore 6 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT SECTION - D Assertion-Reason Type Questions
Explore 25 Videos
- GRAVITATION Book:AAKASH INSTITUTE ENGLISHChapter:GRAVITATION Exercise:ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
Explore 15 Videos
Similar Questions
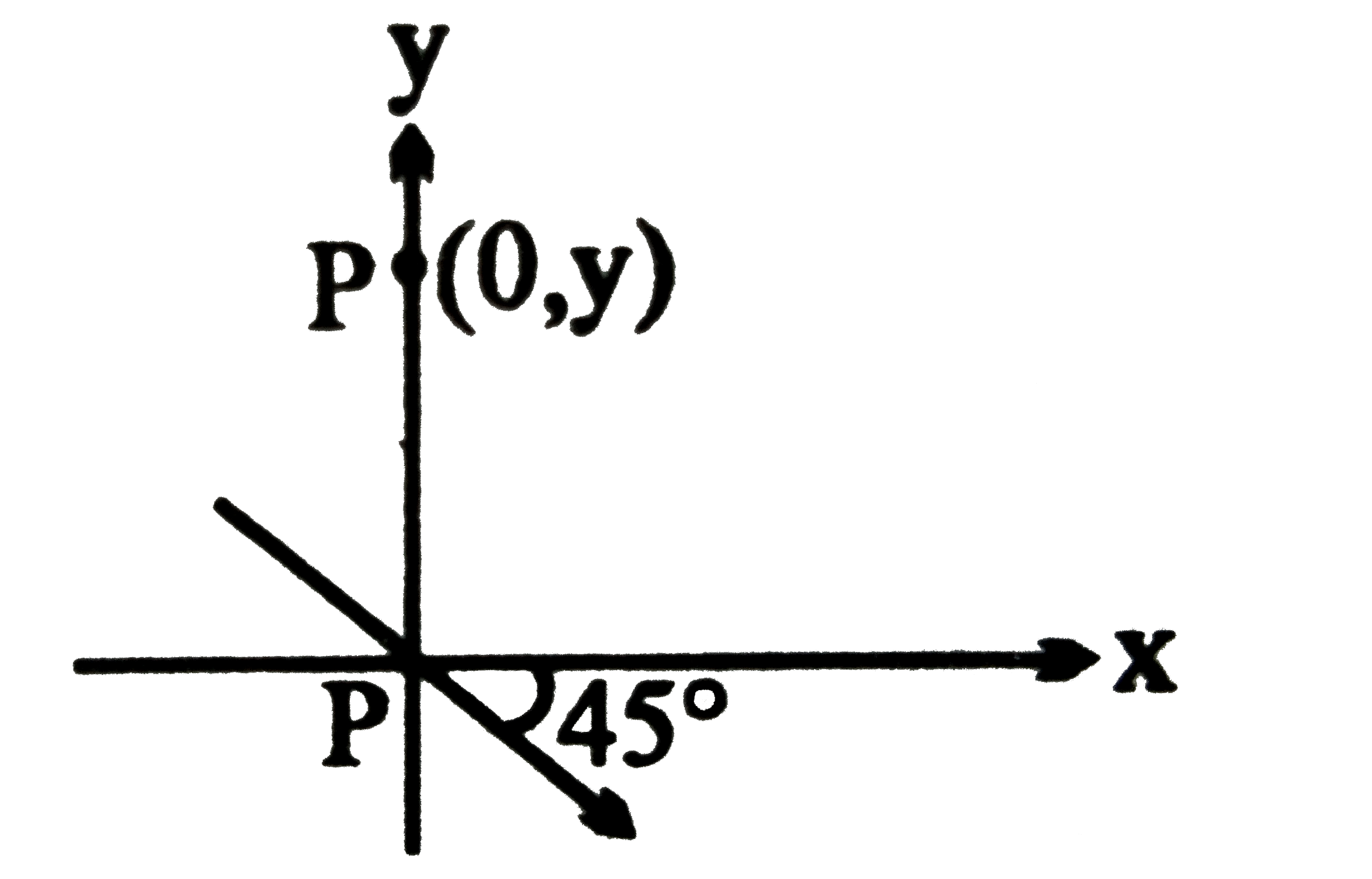
A dipole is placed at origin of coordinate system as shown in figure, find the electric field at point P(0,y)
 .
.
View SolutionA point charge q=−8.0nC is located at the origin. Find the electric field vector at the point x=1.2m,y=−1.6m.
View SolutionAs charge q=1μC is placed at point (1m,2m,4m). Find the electric field at point P(0,−4m,3m)
View SolutionA short electric dipoleis placed along y-axis at the origin. The electric field vector at a point P on x-axis is →E1. The dipole is rotated by π2 at its positin . Now, the electric field vector at point P is →E2. Select the correct alternative(s) :
View SolutionTwo small electric dipoles each of dipole moment pˆi are situated at (0,0,0) and (r,0,0). The electric potential at a point (r2,√3r2,0) is:
View SolutionAn electric dipole is placed at the origin along x-axis.The electric field at any point , whose position vector , makes an angle θ with the x-axis ,makes an angle,
View SolutionIf by shifting the origin at (1,1) the coordinates of a point P become (cosθ,cosϕ) then the original coordinates of P were
View SolutionA point electric dipole of moment →p1=(√3ˆi+ˆj) is held fixed at the origin. Another point electric dipole of moment →p2 held at the point A (+a, 0, 0) will have minimum potential energy, if its orientation is given by the vector
View SolutionThe potentaial function of an electrostatic field is given by V=2x2. Determine the electric field strength at the point (2m,0,3m).
View SolutionAn electric dipole of moment rp=(ˆi+2ˆj)×10−28Cm is at origin. The electric field at point ( 2,4) due to the dipole is parallelto
View Solution