The electric field in a region is radially outward and varies with distance r as E=250 r ( volt per square metre).Calculate the charge contained in a sphere of radius 0.2 m centere at the origin.
To solve the problem, we will use Gauss's Law, which relates the electric field to the charge enclosed by a surface. Here's the step-by-step solution:
Step 1: Understand the Electric Field
The electric field E is given as:
E=250r(in volts per meter)
This indicates that the electric field varies linearly with the distance r from the origin.
Step 2: Define the Gaussian Surface
We will consider a spherical Gaussian surface of radius r=0.2m centered at the origin. The surface area S of a sphere is given by:
S=4πr2
Step 3: Calculate the Surface Area
Substituting r=0.2m:
S=4π(0.2)2=4π(0.04)=0.16πm2
Step 4: Apply Gauss's Law
Gauss's Law states:
ΦE=Qϵ0
where ΦE is the electric flux through the Gaussian surface, Q is the charge enclosed, and ϵ0 is the permittivity of free space (ϵ0≈8.85×10−12C2/N m2).
The electric flux ΦE can also be expressed as:
ΦE=E⋅S
Step 5: Substitute the Electric Field and Surface Area
Substituting E=250r at r=0.2m:
E=250×0.2=50V/m
Now substituting into the flux equation:
ΦE=50⋅(0.16π)=8πV m
Step 6: Relate Flux to Charge
Using Gauss's Law:
8π=Qϵ0
Thus,
Q=8πϵ0
Step 7: Substitute the Value of ϵ0
Substituting ϵ0:
Q=8π(8.85×10−12)≈2.22×10−10C
Final Answer
The charge contained in the sphere of radius 0.2m centered at the origin is approximately:
Q≈2.22×10−10C
---
The electric field E is given as:
E=250r(in volts per meter)
This indicates that the electric field varies linearly with the distance r from the origin.
We will consider a spherical Gaussian surface of radius r=0.2m centered at the origin. The surface area S of a sphere is given by:
S=4πr2
Substituting r=0.2m:
S=4π(0.2)2=4π(0.04)=0.16πm2
Gauss's Law states:
ΦE=Qϵ0
where ΦE is the electric flux through the Gaussian surface, Q is the charge enclosed, and ϵ0 is the permittivity of free space (ϵ0≈8.85×10−12C2/N m2).
ΦE=E⋅S
Substituting E=250r at r=0.2m:
E=250×0.2=50V/m
Now substituting into the flux equation:
ΦE=50⋅(0.16π)=8πV m
Using Gauss's Law:
8π=Qϵ0
Thus,
Q=8πϵ0
Substituting ϵ0:
Q=8π(8.85×10−12)≈2.22×10−10C
The charge contained in the sphere of radius 0.2m centered at the origin is approximately:
Q≈2.22×10−10C
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - TRY YOURSELF
33 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - ASSIGNMENT(SECTION-A) Objective Type Question
45 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
15 Videos
Similar Questions
Electric field in a region of space is radially outward from origin and varies with distance 'r' from origin as E = kr. Find the charge enclosed in a sphere of radius 'a' centred at origin.
View SolutionThe electric field in a region is radially outward with magnitude E = 2r. The charge contained in a sphere of radius a = 2m centerd at the origin is 4xπε0. Find the value of x.
View Solution
Knowledge Check
Electric field intensity (E) due to an electric dipole varies with distance (r ) from the point of the center of dipole as :
A1rand1r2B1r2and1rC1r3and1r3D1r3and1r2
The electric field in a region is radially outward with magnitude E=Ar. Find the charge contained in a sphere of radius a centred at the origin. Take A=100Vm−2 and a=20.0cm.
View SolutionThe electric field in a certain region is acting radially outwards and is given by E=Ar.A charge contained in a sphere of radius 'a' centred at the origin of the field, will given by
View SolutionThe electric field in aregion is radially ourward with magnitude E=Ar. Find the charge contained in a sphere of radius a centred at the origin. Take A=100Vm−2 and a=20.0cm.
View SolutionThe electric field in a region is radially outward with magnitude E=Aγ0. The charge contained in a sphere of radius γ0 centered at the origin is
View SolutionThe electric field in a region is directed outward and is proportional to the distance r from the origin, Taking the electric potential at origin to be zero,
View SolutionThe electric field in a region is radially outwards with magnitude E=αr/ε0. IN a sphere of radius R centered at the origin, calculate the value of charge in coulombs α=5π if V/m2 and R=(310)1/3m.
View SolutionAn electric field 'E' whose direction is radially outward varies as distance from origin 'r' as shown in the graph E is taken as positive if its direction is away from the origin. Then the work done by electric field on a 2 C charge if it is taken from (1,1,0) to (3,0,0) is :
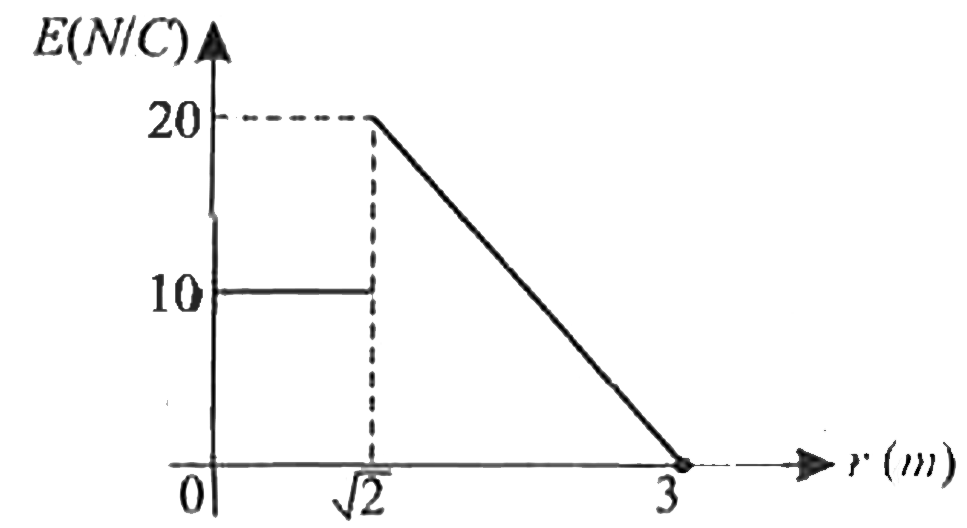
View Solution
