Calculate the magnitude of the electric field which can just balance a deuteron of mass 3.2×10−27kg
To calculate the magnitude of the electric field that can just balance a deuteron of mass 3.2×10−27 kg, we will follow these steps:
Step 1: Identify the Forces Acting on the Deuteron
The deuteron experiences two main forces:
1. The gravitational force (FG) acting downwards.
2. The electric force (FE) acting upwards when an electric field is applied.
Step 2: Write the Expression for Gravitational Force
The gravitational force can be calculated using the formula:
FG=m⋅g
where:
- m=3.2×10−27kg (mass of the deuteron)
- g=9.8m/s2 (acceleration due to gravity)
Step 3: Calculate the Gravitational Force
Substituting the values into the formula:
FG=3.2×10−27kg×9.8m/s2
FG=3.136×10−26N
Step 4: Write the Expression for Electric Force
The electric force acting on the deuteron in an electric field E is given by:
FE=Q⋅E
where Q is the charge of the deuteron. The charge of a deuteron is approximately the same as that of a proton, which is:
Q=1.6×10−19C
Step 5: Set the Forces Equal to Each Other
To balance the deuteron, the electric force must equal the gravitational force:
FE=FG
Thus,
Q⋅E=m⋅g
Step 6: Solve for the Electric Field E
Rearranging the equation to solve for E:
E=m⋅gQ
Step 7: Substitute the Values
Substituting the known values:
E=3.2×10−27kg×9.8m/s21.6×10−19C
Step 8: Calculate the Electric Field
Calculating the numerator:
3.2×10−27×9.8=3.136×10−26N
Now substituting this into the equation for E:
E=3.136×10−261.6×10−19≈1.96×10−7N/C
Step 9: Final Result
Thus, the magnitude of the electric field that can just balance the deuteron is:
E≈1.96×10−7N/C
---
The deuteron experiences two main forces:
1. The gravitational force (FG) acting downwards.
2. The electric force (FE) acting upwards when an electric field is applied.
The gravitational force can be calculated using the formula:
FG=m⋅g
where:
- m=3.2×10−27kg (mass of the deuteron)
- g=9.8m/s2 (acceleration due to gravity)
Substituting the values into the formula:
FG=3.2×10−27kg×9.8m/s2
FG=3.136×10−26N
The electric force acting on the deuteron in an electric field E is given by:
FE=Q⋅E
where Q is the charge of the deuteron. The charge of a deuteron is approximately the same as that of a proton, which is:
Q=1.6×10−19C
To balance the deuteron, the electric force must equal the gravitational force:
FE=FG
Thus,
Q⋅E=m⋅g
Rearranging the equation to solve for E:
E=m⋅gQ
Substituting the known values:
E=3.2×10−27kg×9.8m/s21.6×10−19C
Calculating the numerator:
3.2×10−27×9.8=3.136×10−26N
Now substituting this into the equation for E:
E=3.136×10−261.6×10−19≈1.96×10−7N/C
Thus, the magnitude of the electric field that can just balance the deuteron is:
E≈1.96×10−7N/C
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTE ENGLISHChapter:ELECTRIC CHARGES AND FIELDS Exercise:TRY YOURSELF
Explore 32 Videos
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTE ENGLISHChapter:ELECTRIC CHARGES AND FIELDS Exercise:ASSIGNMENT(SECTION-A) Objective Type Question
Explore 45 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
Explore 15 Videos
Similar Questions
Calculate the electric field strength which is required to just support a water drop of mass 10−3 kg and having a charge 1.6×10−19C.
View SolutionCalculate the magnitude and direction of the electric field at a point P which is 30 cm to the right of a point charge Q=−3.0×10−6C
View SolutionA beam of charged particle, having kinetic energy 103eV, contains masses 8×10−27kgand1.6×10−26kg emerge from the end of an accelerator tube. There is a plate at distance 102m from the end of the tube and placed perpendicular to the beam. Calculate the magnitude of the smallest magnetic field which can prevent the beam from striking the plate.
View SolutionFind the magnitude of the electric field at a point 4 cm away from a line charge of density 2×10−6Cm−1.
View SolutionImagine a short diploe at the center of a spherical surface. If the magnitude of the electric field at a certain point on the surface of he sphere is 10NC_1 then which of the following cannot be the magnitude of the electric field anywhere on the surface of the sphere?
View SolutionA particle having a charge+3×10−9C is placed in a uniform electric field directed toward left. It is released from rest and moves a distance of 5 cm after which its kinetic energy is found to be 4.5×10−5J.
(a) Calcnalate the work done by the electrical force on the particle
(b) Calculate the magnitude of the electric field.
(c) Calculate the potential of starting point with respect to the end point of particle's motion.
View SolutionThe magnitude and direction of the electric field at point P can be best represented by
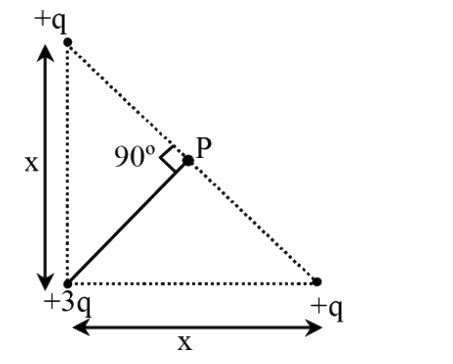
View SolutionCalculate the electric field strength required just to support a water drop of mass 10−7kg having a charge 1.6×10−19C
View SolutionA proton goes undflected in a crossed and magnetic field (the fields are perpendicular to each other) at a speed of 2.0X105ms−1. The velocity is perpendicular to both the fields. When the electric field is switched off, the proton moves along a circle of radius 4.0 cm. Find the magnitudes of the electric and the magnetic fields. take the mass of the proton =1.6X10−27 kg.
View SolutionCalculate the electric field intensity which would be just sufficient to balance the weight of a particle of charge −10μC and mass 10 mg. (Take g=10ms2)
View Solution