Calculate the electric field intensity which would be just sufficient to balance the weight of a particle of charge −10μC and mass 10 mg. (Take g=10ms2)
To solve the problem of calculating the electric field intensity that would balance the weight of a charged particle, we can follow these steps:
Step 1: Identify the given values
- Charge of the particle, q=−10μC=−10×10−6C
- Mass of the particle, m=10mg=10×10−3g=10×10−6kg
- Acceleration due to gravity, g=10m/s2
Step 2: Calculate the weight of the particle
The weight W of the particle can be calculated using the formula:
W=m⋅g
Substituting the values:
W=(10×10−6kg)⋅(10m/s2)=10×10−5N=10−4N
Step 3: Relate the electric field intensity to the weight
The electric force F acting on the charged particle in an electric field E is given by:
F=q⋅E
To balance the weight of the particle, we set the electric force equal to the weight:
q⋅E=W
Step 4: Solve for electric field intensity E
Rearranging the equation gives:
E=Wq
Substituting the values we have:
E=10−4N−10×10−6C
Calculating this gives:
E=10−4−10×10−6=10−4−10−5=−10N/C
Step 5: Interpret the result
The negative sign indicates that the direction of the electric field is opposite to the direction of the force due to the negative charge. Therefore, the electric field intensity that would balance the weight of the particle is:
E=10N/C(downward)
Final Answer
The electric field intensity required to balance the weight of the particle is 10N/C directed downward.
---
- Charge of the particle, q=−10μC=−10×10−6C
- Mass of the particle, m=10mg=10×10−3g=10×10−6kg
- Acceleration due to gravity, g=10m/s2
The weight W of the particle can be calculated using the formula:
W=m⋅g
Substituting the values:
W=(10×10−6kg)⋅(10m/s2)=10×10−5N=10−4N
The electric force F acting on the charged particle in an electric field E is given by:
F=q⋅E
To balance the weight of the particle, we set the electric force equal to the weight:
q⋅E=W
Rearranging the equation gives:
E=Wq
Substituting the values we have:
E=10−4N−10×10−6C
Calculating this gives:
E=10−4−10×10−6=10−4−10−5=−10N/C
The negative sign indicates that the direction of the electric field is opposite to the direction of the force due to the negative charge. Therefore, the electric field intensity that would balance the weight of the particle is:
E=10N/C(downward)
The electric field intensity required to balance the weight of the particle is 10N/C directed downward.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Problems
22 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
Calculate the electric field intensity E which would be just sufficient to balance the wight of an electron. If this electric field is produced by a second electron located below the first one what would be the distance between them? [Given: e=1.6×10−19C,m=9.1×10−31kg and g=9.8m/s2]
View SolutionCalculate the electric field strength required just to support a water drop of mass 10−7kg having a charge 1.6×10−19C
View SolutionWhat is the weight of a block of mass 10.5 kg ? Take g=10ms−2
View SolutionCalculate the magnitude of the electric field which can just balance a deuteron of mass 3.2×10−27kg
View SolutionCalculate the magnitude of the electric field which can just balance a deuteron of mass 3.2×10−27kg
View SolutionCalculate the electric field strength which is required to just support a water drop of mass 10−3 kg and having a charge 1.6×10−19C.
View SolutionCalculate the weight of a body of mass 10 kg in newton . Take g=9.8m s−2 .
View SolutionCalculate the weight of a body of mass 10 kg in kgf . Take g=9.8m s−2 .
View SolutionCalculate the weight of :
10.0 g atoms of sodium.
View SolutionIn 1909, Robert Millikan war the firest to find the charge of an electron in his now-famous oil-drop experiment. In that experiment, tiny oil drops were sprayed into a uniform electric field between a horizontal pair of opposite charged plates. The drops were pbserved with a magnitue eyepiece, and the electric field was adjusted so that upward force on some negatively charged oil drops was just sufficient to balance the downward force of gravity. That is, when suspended, upward force qE just equaled mg. Millikan accurately measured the charges on many oil drops and found the values to be whole number multiples of 1.6×10−19C− the charge of the electron. For this, he won the Nobel prize.
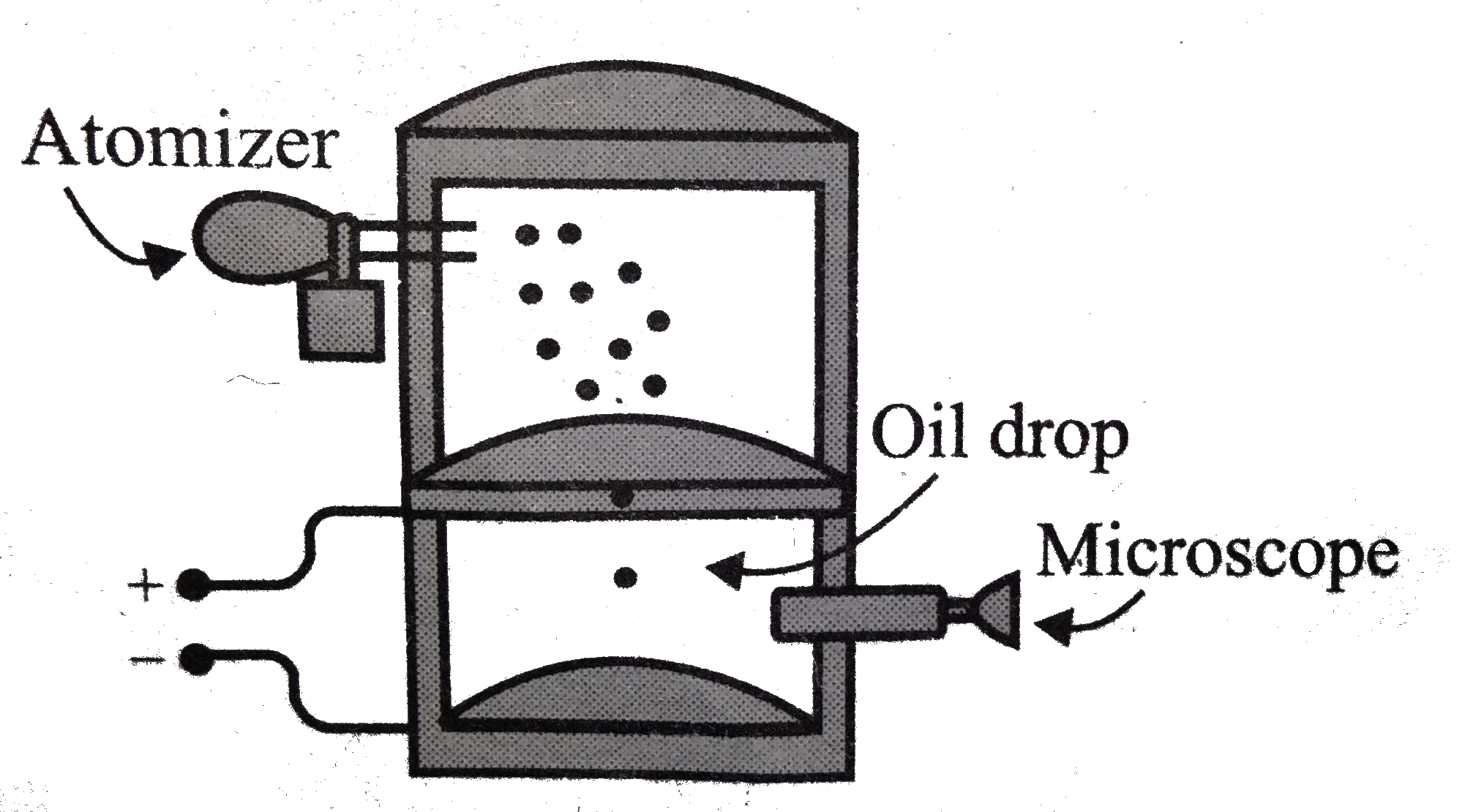
If a drop of mass 1.08×10−14kg remains stationary in an electric field of 1.68×105NC−1, then teh charge of this drop is
View Solution
