A light rope is passed over a pulley such that at its one end a block is attached , and on the other end a boy is climbing up with acceleration g2 relative to rope. Mass of the block is 30 kg and that of the boy is 40 kg. Find the tension and acceleration of the rope .
To solve the problem, we need to analyze the forces acting on both the boy and the block and apply Newton's second law of motion. Let's break down the solution step by step.
Step 1: Define Variables
Let:
- mb=40kg (mass of the boy)
- mblock=30kg (mass of the block)
- g = acceleration due to gravity (approximately 9.81m/s2)
- a1 = acceleration of the block (downward)
- a2 = acceleration of the boy (upward)
Given that the boy is climbing up with an acceleration of g2 relative to the rope, we can express the acceleration of the boy as:
a2=a1+g2
Step 2: Free Body Diagram for the Boy
For the boy climbing up:
- The forces acting on the boy are:
- Tension T acting upward
- Weight Wb=mb⋅g=40g acting downward
Using Newton's second law:
T−40g=mb⋅a2
Substituting mb:
T−40g=40a2
This can be rearranged to:
T=40g+40a2(Equation 1)
Step 3: Free Body Diagram for the Block
For the block hanging down:
- The forces acting on the block are:
- Tension T acting upward
- Weight Wblock=mblock⋅g=30g acting downward
Using Newton's second law:
T−30g=mblock⋅a1
Substituting mblock:
T−30g=30a1
This can be rearranged to:
T=30g+30a1(Equation 2)
Step 4: Set Equations Equal
From Equation 1 and Equation 2, we have:
40g+40a2=30g+30a1
Rearranging gives:
10g=30a1−40a2
This can be simplified to:
3a1−4a2=1g(Equation 3)
Step 5: Substitute for a2
From the relationship a2=a1+g2:
Substituting this into Equation 3:
3a1−4(a1+g2)=1g
Expanding and simplifying:
3a1−4a1−2g=1g
−a1−2g=1g
−a1=3g
Thus,
a1=−3g
This indicates that the block is accelerating downward.
Step 6: Find a2
Now substituting a1 back into the equation for a2:
a2=a1+g2
a2=−3g+g2=−6g2+g2=−5g2
Step 7: Calculate Tension T
Now we can find the tension using either Equation 1 or Equation 2. Using Equation 1:
T=40g+40a2
Substituting a2:
T=40g+40(−5g2)
T=40g−100g=−60g
Final Results
Thus, the tension in the rope is T=−60g (indicating that the tension is acting in the opposite direction to what we assumed) and the accelerations are:
- a1=−3g (downward for the block)
- a2=−5g2 (upward for the boy)
Let:
- mb=40kg (mass of the boy)
- mblock=30kg (mass of the block)
- g = acceleration due to gravity (approximately 9.81m/s2)
- a1 = acceleration of the block (downward)
- a2 = acceleration of the boy (upward)
a2=a1+g2
For the boy climbing up:
- The forces acting on the boy are:
- Tension T acting upward
- Weight Wb=mb⋅g=40g acting downward
T−40g=mb⋅a2
Substituting mb:
T−40g=40a2
This can be rearranged to:
T=40g+40a2(Equation 1)
For the block hanging down:
- The forces acting on the block are:
- Tension T acting upward
- Weight Wblock=mblock⋅g=30g acting downward
T−30g=mblock⋅a1
Substituting mblock:
T−30g=30a1
This can be rearranged to:
T=30g+30a1(Equation 2)
From Equation 1 and Equation 2, we have:
40g+40a2=30g+30a1
10g=30a1−40a2
This can be simplified to:
3a1−4a2=1g(Equation 3)
From the relationship a2=a1+g2:
Substituting this into Equation 3:
3a1−4(a1+g2)=1g
Expanding and simplifying:
3a1−4a1−2g=1g
−a1−2g=1g
−a1=3g
Thus,
a1=−3g
This indicates that the block is accelerating downward.
Now substituting a1 back into the equation for a2:
a2=a1+g2
a2=−3g+g2=−6g2+g2=−5g2
Now we can find the tension using either Equation 1 or Equation 2. Using Equation 1:
T=40g+40a2
Substituting a2:
T=40g+40(−5g2)
T=40g−100g=−60g
Thus, the tension in the rope is T=−60g (indicating that the tension is acting in the opposite direction to what we assumed) and the accelerations are:
- a1=−3g (downward for the block)
- a2=−5g2 (upward for the boy)
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:LAWS OF MOTIONExercise:Illustration
Explore 7 Videos
- LAWS OF MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:LAWS OF MOTIONExercise:TRY YOURSELF
Explore 69 Videos
- KINETIC THEORYBook:AAKASH INSTITUTE ENGLISHChapter:KINETIC THEORYExercise:EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
Explore 10 Videos
- MAGNETISM AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:MAGNETISM AND MATTER Exercise:ASSIGNMENT (SECTION D)
Explore 26 Videos
Similar Questions
A 40 kg boy climbs a rope that passes over an ideal pulley. The other end of the rope is attached to a 60 kg weight placed on the ground. What is the maximum upward acceleration the boy can have without lifting the weight ? If he climbs the rope with upward acceleration 2 g, with what acceleration the weight will rise up ?
View SolutionA block B is tied to one end of a uniform rope R as shown. The mass of block is 2 kg and that of rope is 1 kg. A force F = 15 N is applies at angle 37∘ with vertical. The tension at the mid-point of rope is

View SolutionA rope thrown over a pulley has a on one of its ends and a counterbalancing mass M on its other end. The man whose mass is m, climbs upwards by →△r relative to the ladder and then stops. Ignoring masses of the pulley and the rope, as well as the friction the pulley axis, find the displacement of the centre of mass of this system.
View SolutionA rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
View SolutionA boy and a block, both of same mass, are suspended at the same horizontal level, from each end of a light string that moves over a frictionless pulley as shown. The boy start moving upward with an acceleration 2.5m/s2 relative the rope. If the block is to travel a total distance 10m before reaching at the pulley, the time taken by the block in doing so is equal to:

View SolutionA monkey of mass 'm' climbs up to a rope hung over a fixed pulley with an acceleration g/4. The opposite end of the rope is tied to a block of mass M lying on a rough horizontal plane. The coefficient of friction between the block and horizontal plane is μ. Find the tension in the rope.

View SolutionTow men of masses m1andm2 hold on the opposite ends of a rope passing over a frictionless pulley. The men m1 climbs up the pore with an acceleration of 1.2m/s2 relative to the rope. The mann m2 climbs up the rope with an acceleration of 2m/s2 relative to the rope. Find the tension in the rope if m140kgandm2=60kg. Also find the time after the time after which they will be at same horizontal level if they start from rest and are initially separted by 5 m.
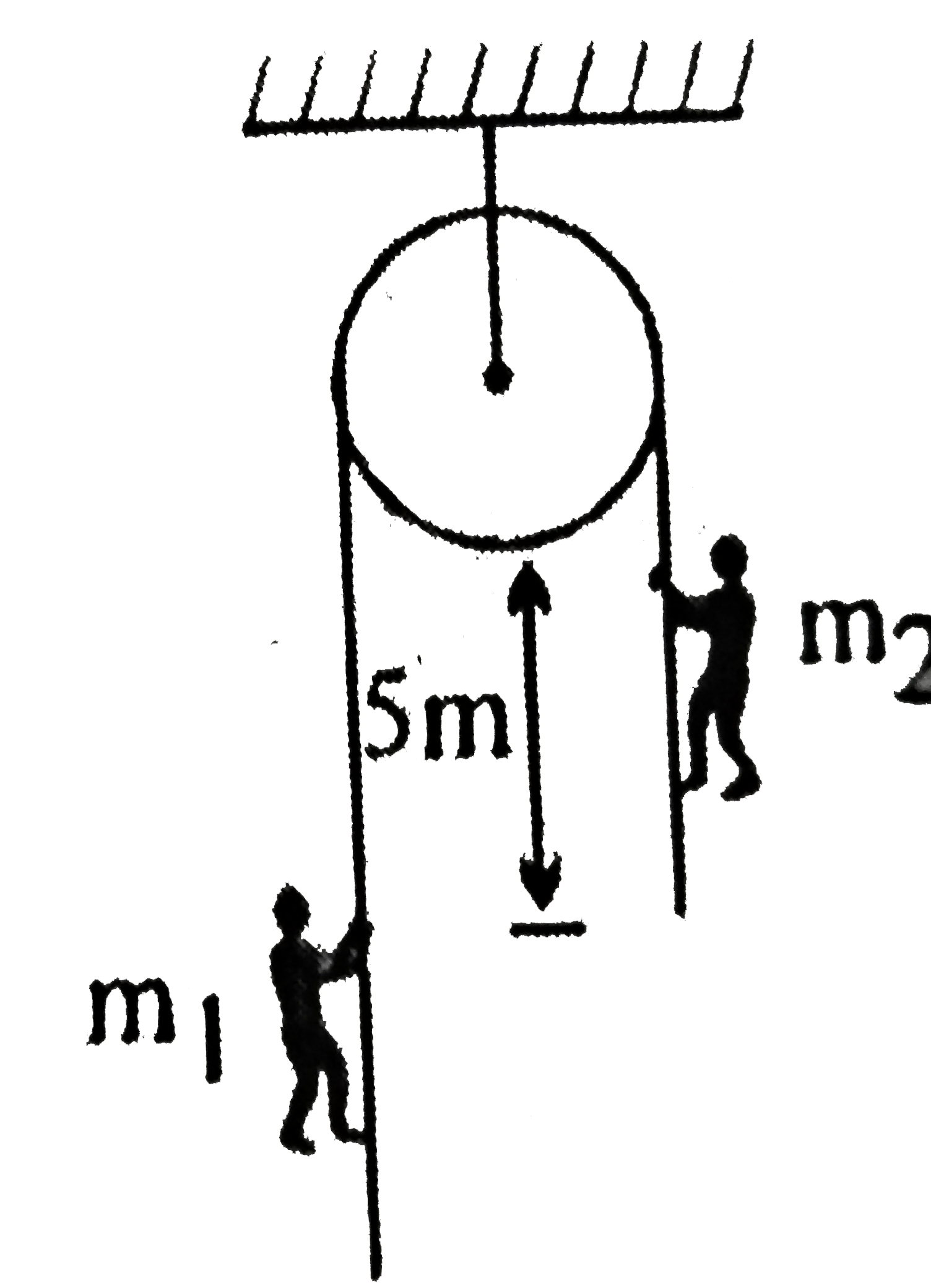
View SolutionA 2 kg block A is attached to one end of a light string that passes over an an ideal pulley and a 1 kg sleeve B slides down the other part of the string with an acceleration of 5m/s2 with respect to the string. Find the acceleration of the block, acceleration of sleeve and tension in the steing. [g=10m/s2]

View SolutionA rope passess over a pulley which is sufficiently high. Two monkeys of equal mass climb the rope from opposite ends, one of them climbing quickly than the other relative to the rope. Assuming that the pulley and the rope are weightless and the rope is in extensible, which of monkeys will reach the top first?
View SolutionIn order to raise a mass of 100 kg, a man of mass 60 kg fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with acceleration 5g/4 relative to the rope. The tension in the rope is (take g=10ms−2)

View Solution
