Question

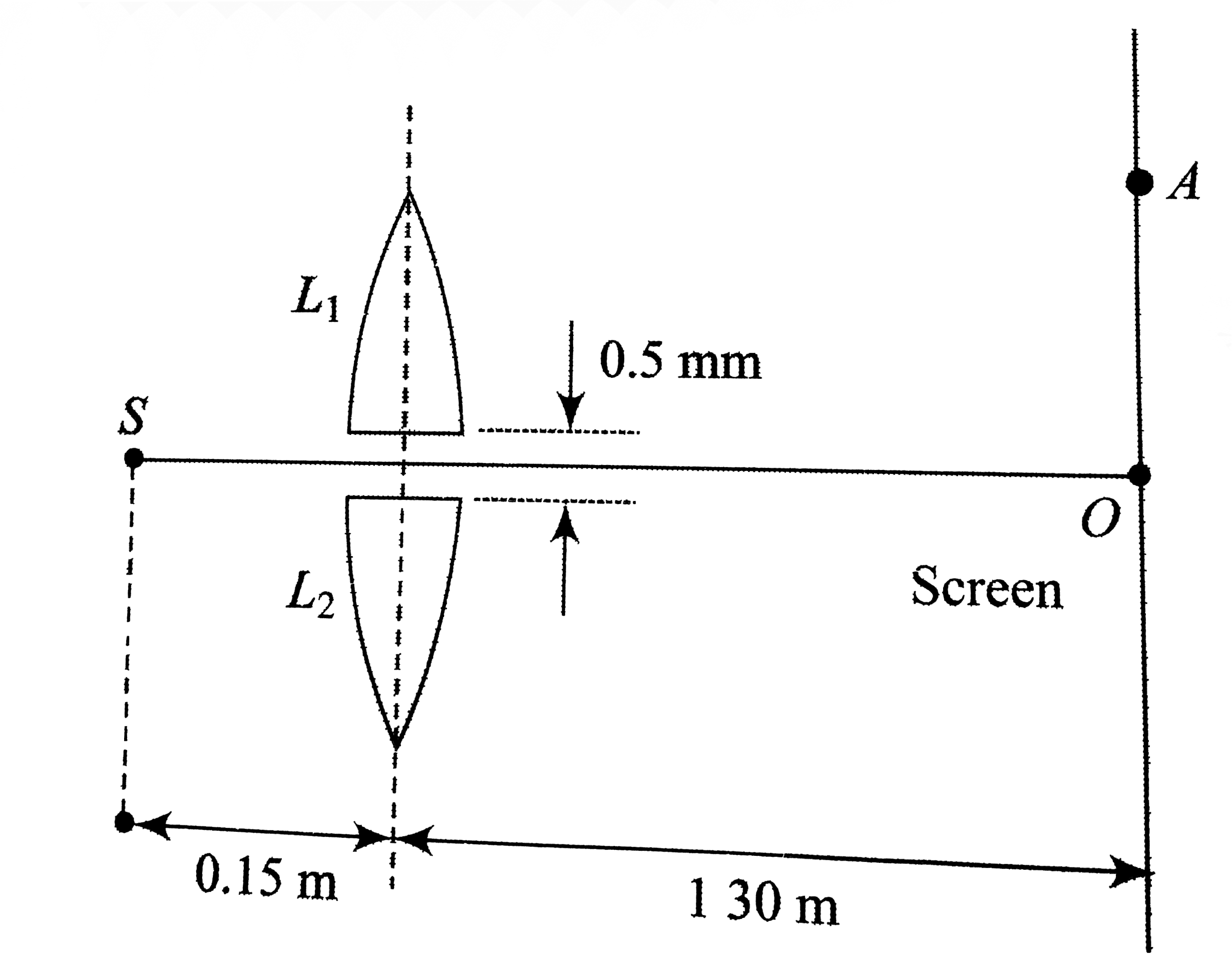
In figure S is a monochromatic point source emitting light of wavelength ${\displaystyle \lambda =500nm}$ A thin lens of circular shape and focal length ${\displaystyle 0.10}$ m is cut into two identical havles ${\displaystyle L_1}$ and ${\displaystyle L_2}$ a plane passing through a diameter. The two havles are placed symmetrically about the central axis SO with a gap of ${\displaystyle 0.5}$ mm. The distance along the axis from S TO${\displaystyle L_1}$ and ${\displaystyle L_2}$ is ${\displaystyle 0.15}$ m. The screen at O is normal to SO.
a. If the third intensity maximum occurs at point A on the screen, find the distance OA.
b. If the gap between, ${\displaystyle L_1}$ and ${\displaystyle L_2}$ is reduced from its original value of ${\displaystyle 0.5}$ mm, will the distance OA increase, decrease, or remain the same ?

Explanation

The axis of the two lens parts are separated by 0.5 mm. the source S is distance 0.25 mm from each of these two axis.
The two lens fragments now form two images S' and S'' at distance given by
`1/v-1/u=1/f`
`rArr=1/v-1/(-0.15)=1/0.1`
or v=+30 cm
Now `m=v/u=(+30)/(-15)=2`
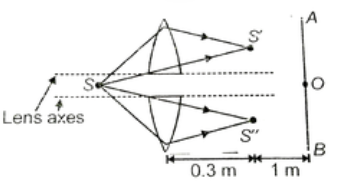The distance of S' and S'' from the axis should by twice the distance of S from the source on the opposite side of the axis (because the magnifications is -2). hence the distance of S' and S'' from the axis are 0.25 x 2 =0.5 mm each . These images now act as coherent sources with a distance d (=15 mm) between them. the screen is now distant 1 m from the two sources (this is D)
Now, the fringe width `beta` is given by
`beta =(lambdaD)/d=(500xx10^(-9)xx1)/(1.5xx10^(-3))=0.33 mm`
(i) Now OA=`3beta`
=0.33x 3
=1 min
(ii) When the distance between the lenses is reduced, it reduces d and hence increases `beta` and thereby OA increases.