Find the mutual inductance between two coaxial loops of radii R and r (R gtgt r) with separation between the centre x.
To find the mutual inductance M between two coaxial loops of radii R (larger loop) and r (smaller loop) with a separation x between their centers, we can follow these steps:
Step 1: Understanding the System
We have two coaxial circular loops:
- The larger loop has a radius R.
- The smaller loop has a radius r.
- The distance between the centers of the loops is x.
Step 2: Current in the Larger Loop
Let a current I flow through the larger loop (radius R). This current will create a magnetic field at the center of the smaller loop.
Step 3: Magnetic Field at the Center of the Smaller Loop
The magnetic field B at the center of the smaller loop due to the larger loop is given by the formula:
B=μ0I2R(for a circular loop)
However, since the distance between the loops is x, we need to adjust this formula to account for the separation. The magnetic field at the center of the smaller loop can be approximated as:
B=μ0I⋅2πR24π(R2+x2)3/2
Step 4: Area of the Smaller Loop
The area A of the smaller loop is given by:
A=πr2
Step 5: Magnetic Flux through the Smaller Loop
The magnetic flux Φ through the smaller loop is given by:
Φ=B⋅A
Substituting the expressions for B and A:
Φ=(μ0I⋅2πR24π(R2+x2)3/2)⋅(πr2)
This simplifies to:
Φ=μ0I⋅2π2R2r24(R2+x2)3/2
Step 6: Mutual Inductance Formula
The mutual inductance M is defined as:
M=ΦI
Substituting the expression for Φ:
M=μ0⋅2π2R2r24(R2+x2)3/2
This can be further simplified to:
M=μ0πr22(R2+x2)3/2⋅R2
Final Expression for Mutual Inductance
Thus, the mutual inductance M between the two coaxial loops is:
M=μ0πr2R22(R2+x2)3/2
We have two coaxial circular loops:
- The larger loop has a radius R.
- The smaller loop has a radius r.
- The distance between the centers of the loops is x.
Let a current I flow through the larger loop (radius R). This current will create a magnetic field at the center of the smaller loop.
The magnetic field B at the center of the smaller loop due to the larger loop is given by the formula:
B=μ0I2R(for a circular loop)
However, since the distance between the loops is x, we need to adjust this formula to account for the separation. The magnetic field at the center of the smaller loop can be approximated as:
B=μ0I⋅2πR24π(R2+x2)3/2
The area A of the smaller loop is given by:
A=πr2
The magnetic flux Φ through the smaller loop is given by:
Φ=B⋅A
Substituting the expressions for B and A:
Φ=(μ0I⋅2πR24π(R2+x2)3/2)⋅(πr2)
This simplifies to:
Φ=μ0I⋅2π2R2r24(R2+x2)3/2
The mutual inductance M is defined as:
M=ΦI
Substituting the expression for Φ:
M=μ0⋅2π2R2r24(R2+x2)3/2
This can be further simplified to:
M=μ0πr22(R2+x2)3/2⋅R2
Thus, the mutual inductance M between the two coaxial loops is:
M=μ0πr2R22(R2+x2)3/2
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Try Yourself
42 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - A)
55 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
Find the mutual inductance between two rectangular loops, shown in the figure.
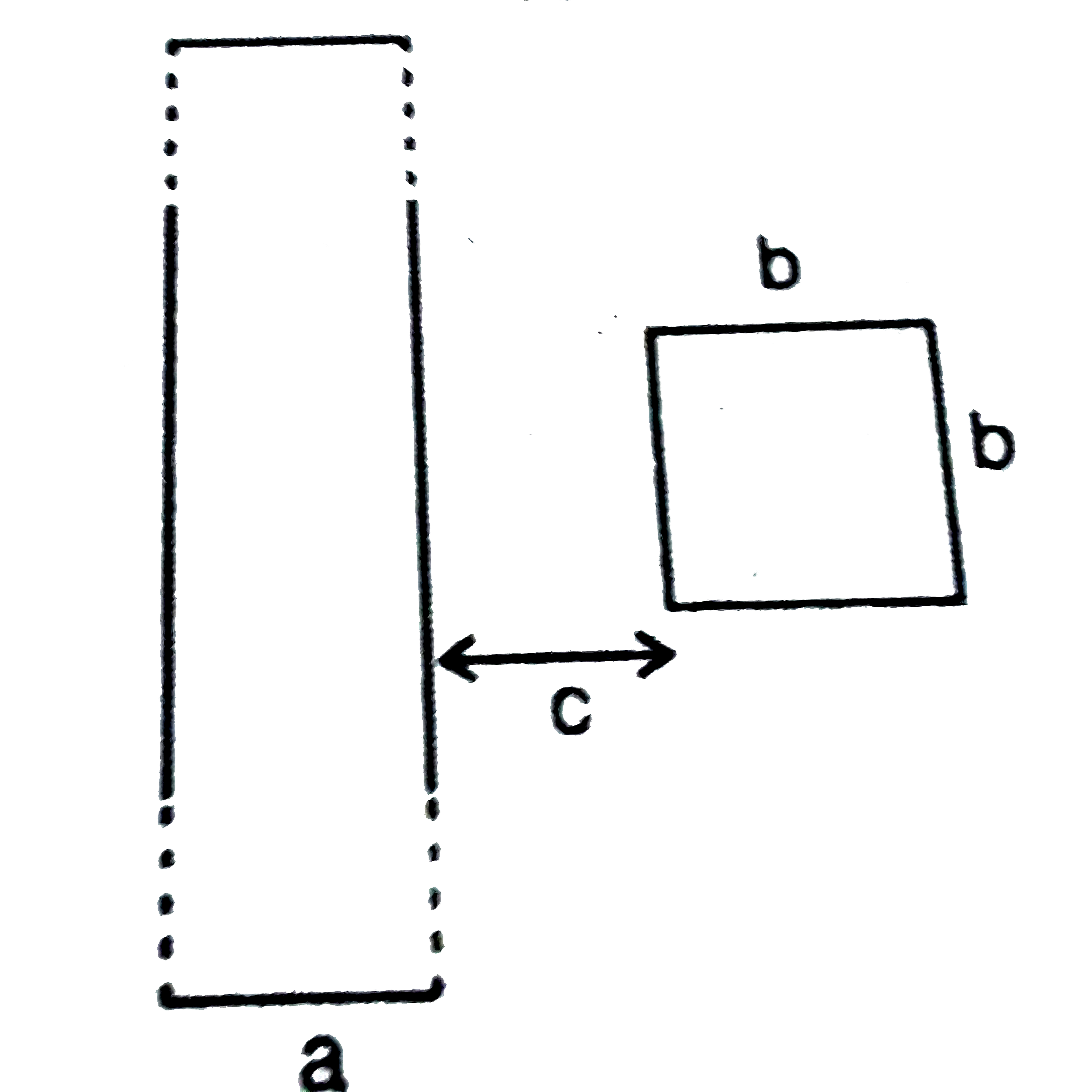
View SolutionFind the mutual inductance between two rectangular loops, shown in the figure.

View SolutionDefine mutual inductance between two long coaxial solenoids. Find out the expression for the mutual of inner solenoid of length 1 having the radius r1 and the number of turns n1 per unit length due to the second other solenoid of same length and n2 number of turns per unit length.
View SolutionThe approximate formula expressing the formula of mutual inductance of two coaxial loops of the same redius a when their centers are separated by a distance l with l>>a is
View SolutionA: The mutual Induction between the two coils infinitely apart is zero. R: If the mutual induction between the two coils is zero, it means that their self inductances are also zero.
View SolutionThere is a the system of two concentric loops of radii r and R (R>>r) . Find the mutual inductance of the system . If the loops have currents of same magnitude i0 lgnore the effect of self inductance .
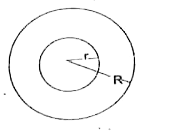
View SolutionFigure shows two concentric loops of radii R and r (R gtgt r). A current i is passed through the outer loop. Find the flux linked with inner loop and the mutual inductance of the arrangement.
View SolutionFind mutual inductance if we have a square loop of side r instead of a small circular loop of side r at the centre of bigger circular loop.
View SolutionThe gravitational force between two objects is proportional to 1/R (and not as 1/R2) where R is separation between them, then a particle in circular orbit under such a force would have its orbital speed v proportional to
View SolutionThe gravitational force between two objects is proportional to 1/R (and not as 1/R2) where R is separation between them, then a particle in circular orbit under such a force would have its orbital speed v proportional to
View Solution
