Find mutual inductance if we have a square loop of side r instead of a small circular loop of side r at the centre of bigger circular loop.
To find the mutual inductance M when a square loop of side r is placed at the center of a larger circular loop of radius R, we can follow these steps:
Step 1: Understand the Configuration
We have a larger circular loop with radius R carrying a current I. At the center of this loop, we place a square loop with side r.
Step 2: Determine the Magnetic Field at the Center of the Circular Loop
The magnetic field B at the center of a circular loop carrying current I is given by the formula:
B=μ0I2R
where μ0 is the permeability of free space.
Step 3: Calculate the Magnetic Flux through the Square Loop
The magnetic flux Φ through the square loop is given by:
Φ=B⋅A
where A is the area of the square loop. The area A of the square loop is:
A=r2
Since the angle θ between the magnetic field and the area vector is 0∘, we have:
Φ=B⋅A=B⋅r2
Substituting the expression for B:
Φ=(μ0I2R)⋅r2
Step 4: Relate Magnetic Flux to Mutual Inductance
The mutual inductance M is defined by the relationship:
Φ=M⋅I
From the previous step, we have:
Φ=μ0Ir22R
Step 5: Solve for Mutual Inductance
Setting the two expressions for Φ equal to each other:
M⋅I=μ0Ir22R
Dividing both sides by I (assuming I≠0):
M=μ0r22R
Final Result
Thus, the mutual inductance M when a square loop of side r is placed at the center of a larger circular loop of radius R is:
M=μ0r22R
---
We have a larger circular loop with radius R carrying a current I. At the center of this loop, we place a square loop with side r.
The magnetic field B at the center of a circular loop carrying current I is given by the formula:
B=μ0I2R
where μ0 is the permeability of free space.
The magnetic flux Φ through the square loop is given by:
Φ=B⋅A
where A is the area of the square loop. The area A of the square loop is:
A=r2
Since the angle θ between the magnetic field and the area vector is 0∘, we have:
Φ=B⋅A=B⋅r2
Φ=(μ0I2R)⋅r2
The mutual inductance M is defined by the relationship:
Φ=M⋅I
From the previous step, we have:
Φ=μ0Ir22R
Setting the two expressions for Φ equal to each other:
M⋅I=μ0Ir22R
Dividing both sides by I (assuming I≠0):
M=μ0r22R
Thus, the mutual inductance M when a square loop of side r is placed at the center of a larger circular loop of radius R is:
M=μ0r22R
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - A)
55 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - B)
22 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
15 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
A square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionFind the magnetic field at the centre of the circular loop shown in figure.

View SolutionFind the mutual inductance between two rectangular loops, shown in the figure.
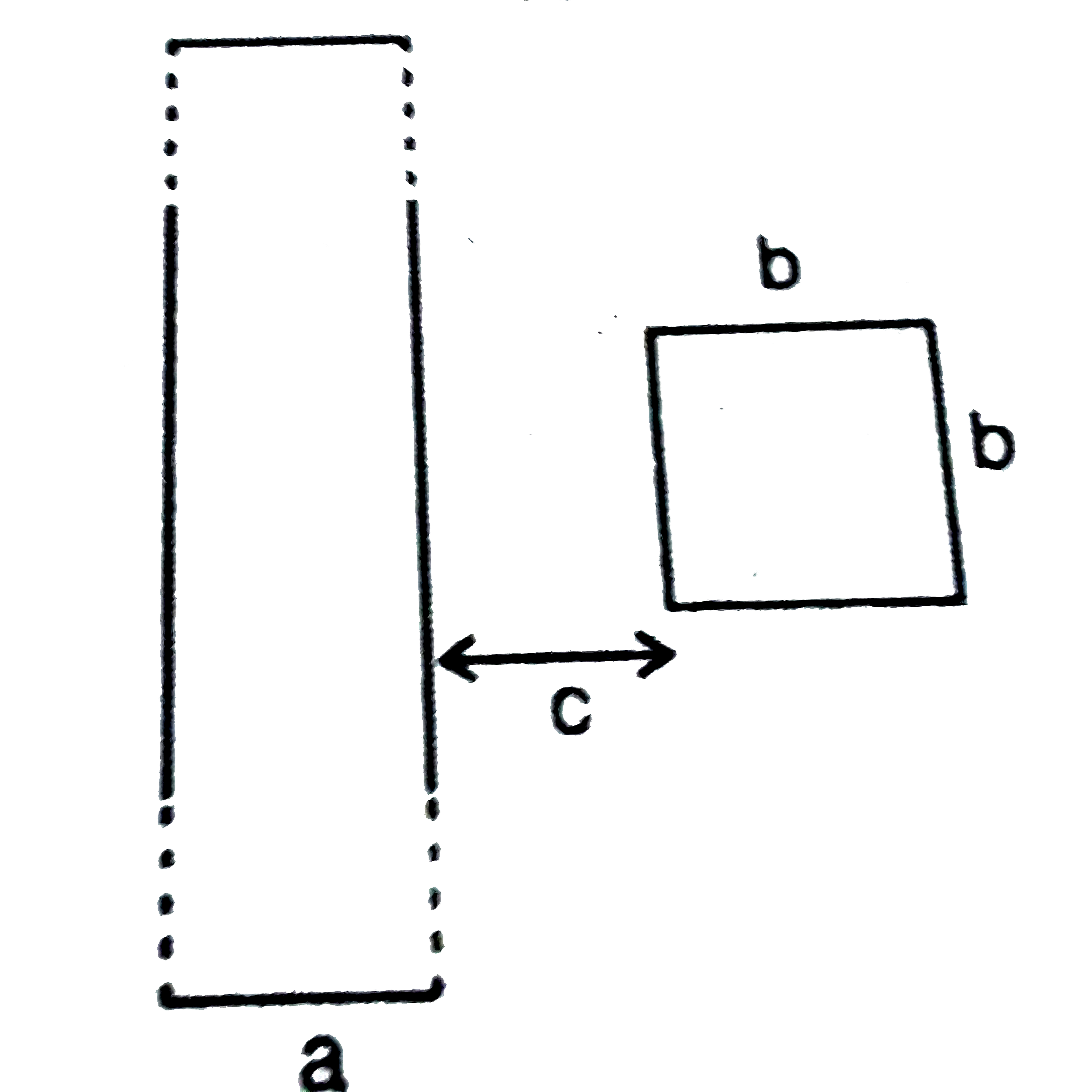
View SolutionFind the mutual inductance between two rectangular loops, shown in the figure.

View SolutionFind the mutual inductance of a straight long wire and a rectangular loop, as shown in the figure.
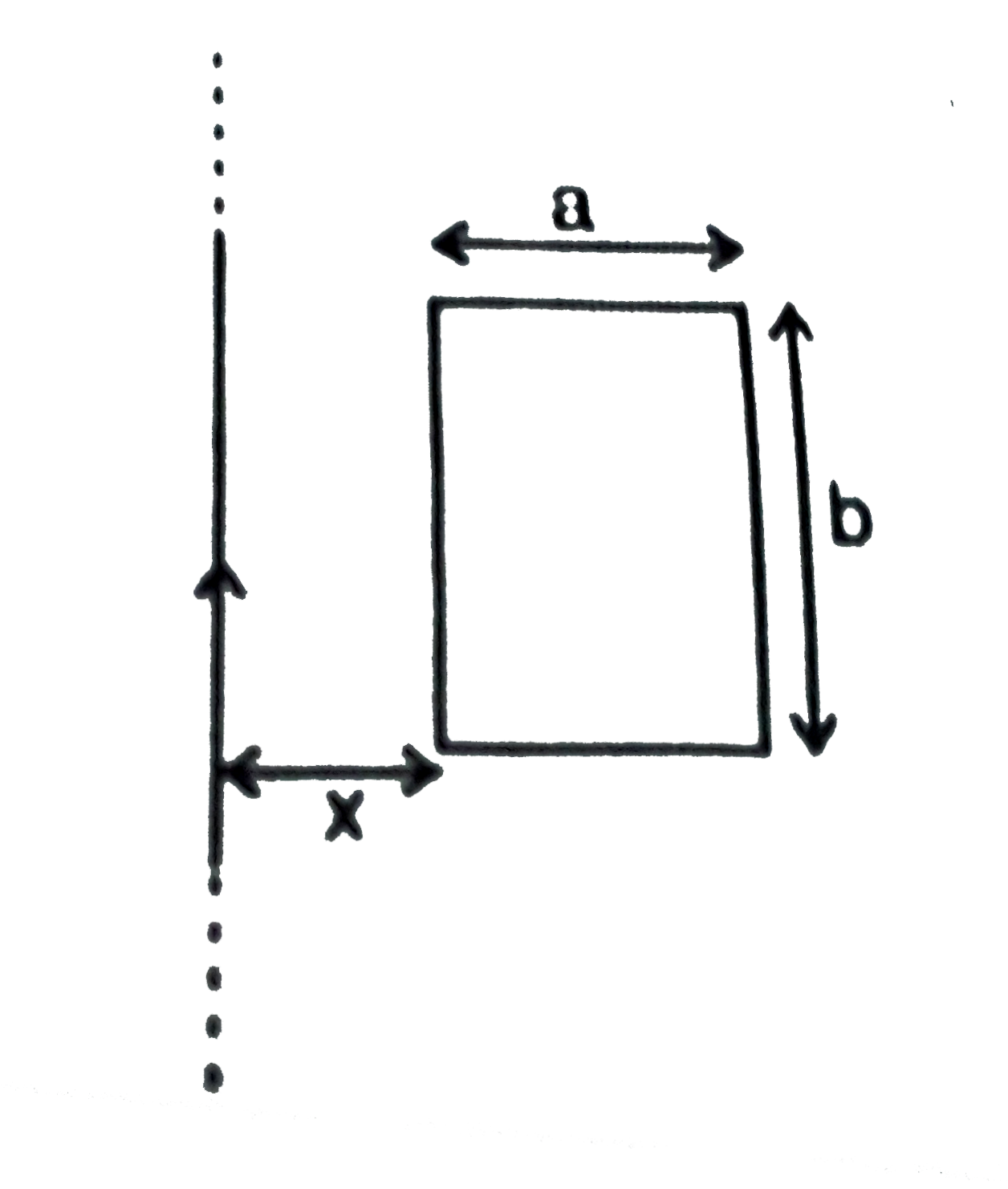
View SolutionFind the mutual inductance of a straight long wire and a rectangular loop, as shown in the figure.

View SolutionFind the mutual inductance between two coaxial loops of radii R and r (R gtgt r) with separation between the centre x.
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionIn the figure, the current l enters the circular loop of uniform wire of radius r at A and leaves it at B. The magnetic field of the centre of circular loop is

View Solution
