A converging beam of light is incident on a concave lens of focal length 20 cm. In the absence of the lens, the beam converges at a point 10 m behind the lens. Find where the beam will converge/diverge after refraction.
To solve the problem step by step, we will use the lens formula for thin lenses, which is given by:
1f=1v−1u
Where:
- f is the focal length of the lens,
- v is the image distance (where the light converges or diverges),
- u is the object distance (the distance of the incoming light beam from the lens).
Step 1: Identify the given values
- Focal length of the concave lens, f=−20 cm (negative because it is a concave lens).
- The distance where the beam converges in the absence of the lens, u=10 m = 1000 cm (positive because it is measured from the lens towards the incoming light).
Step 2: Apply the lens formula
We need to find v using the lens formula:
1f=1v−1u
Substituting the known values:
1−20=1v−11000
Step 3: Rearranging the equation
Rearranging the equation to isolate 1v:
1v=1−20+11000
Step 4: Finding a common denominator
To combine the fractions, we need a common denominator. The least common multiple of 20 and 1000 is 1000:
1−20=−501000
Now substituting back into the equation:
1v=−501000+11000=−50+11000=−491000
Step 5: Calculate v
Now, we take the reciprocal to find v:
v=1000−49≈−20.41 cm
Conclusion
The negative sign indicates that the image formed is virtual and located on the same side as the object (the incoming light). Therefore, the beam will diverge at approximately 20.41 cm behind the lens.
---
- f is the focal length of the lens,
- v is the image distance (where the light converges or diverges),
- u is the object distance (the distance of the incoming light beam from the lens).
- Focal length of the concave lens, f=−20 cm (negative because it is a concave lens).
- The distance where the beam converges in the absence of the lens, u=10 m = 1000 cm (positive because it is measured from the lens towards the incoming light).
We need to find v using the lens formula:
Rearranging the equation to isolate 1v:
To combine the fractions, we need a common denominator. The least common multiple of 20 and 1000 is 1000:
Now, we take the reciprocal to find v:
The negative sign indicates that the image formed is virtual and located on the same side as the object (the incoming light). Therefore, the beam will diverge at approximately 20.41 cm behind the lens.
Similar Questions
A converging beam of light is incident on a concave lens. The beam converges behind the lens at 15 cm from its centre, in the absence of the lens. Select the correct alternative
View SolutionA converging lens of focal length 40 cm is kept in contact with a diverging lens of focal length 30 cm. Find the focal length of the combination.
View Solution
Knowledge Check
A convergent beam of light passes through a diverging lens of focal length 0.2m and comes to focus at a distance of 0.3m behind the lens. Find the position of the point at which the beam would converge in the absence of the lens.
A0.12mB0.6mC0.3mD0.15m
A converging beam of rays is incident on a diverging thin lens. Having passed through the lens the rays intersect at a point 15cm from the lens. If lens is removed the point where the rays meet will move 5cm closer towards the mounting that holds the lens. The focal length of lens is
View SolutionA parallel beam of light is incident on a lens of focal length 10 cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. Find the distance of the final image from the lens.
 .
.
View SolutionFigure given below shows a beam of light converging at point P. When a concave lens of focal length 16cm is introduced in the path of the beam at a place O shown by dotted line such that OP becomes the axis of the lens, the beam converges at a distance x from the lens. The value x will be equal to
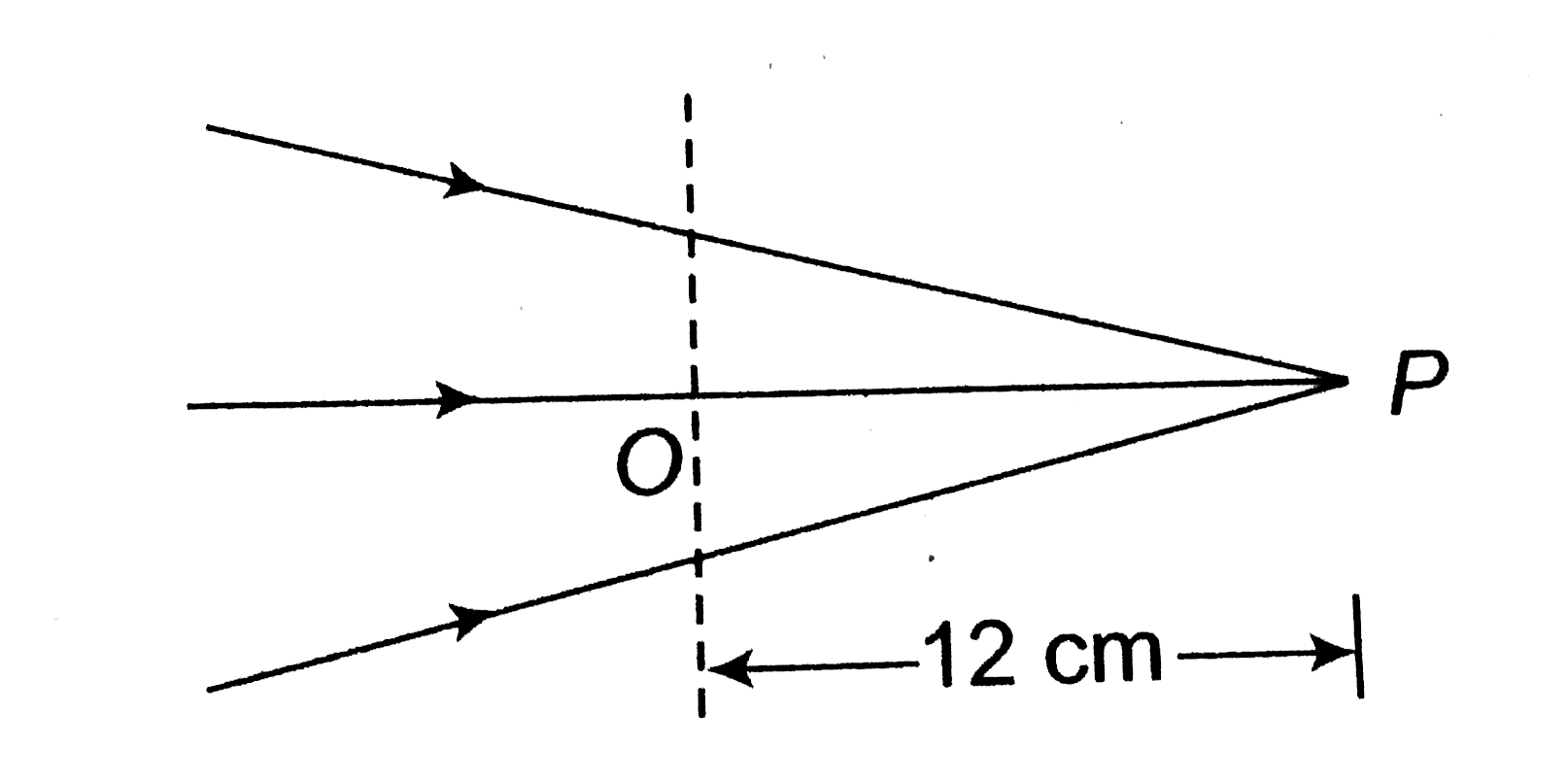
View SolutionA converging beam of rays is incident on a diverging lens. Having passed through the lens the rays intersect at a point 15cm from the lens. If the lens is removed, the point where the rays meet, move 5cm closer to the mounting that holds the lens. Find the focal length of the lens.
View SolutionConverging and diverging beams of light
View SolutionAn object O is kept infront of a converging lens of focal length 30 cm behind which there is a plane mirror at 15 cm from the lens.
_E01_080_Q01.png)
View SolutionA converging lens of focal length 5.0cm is placed in contact
with a diverging lens of focal length 10.0cm. Find the combined focal length of
the system.
View Solution
