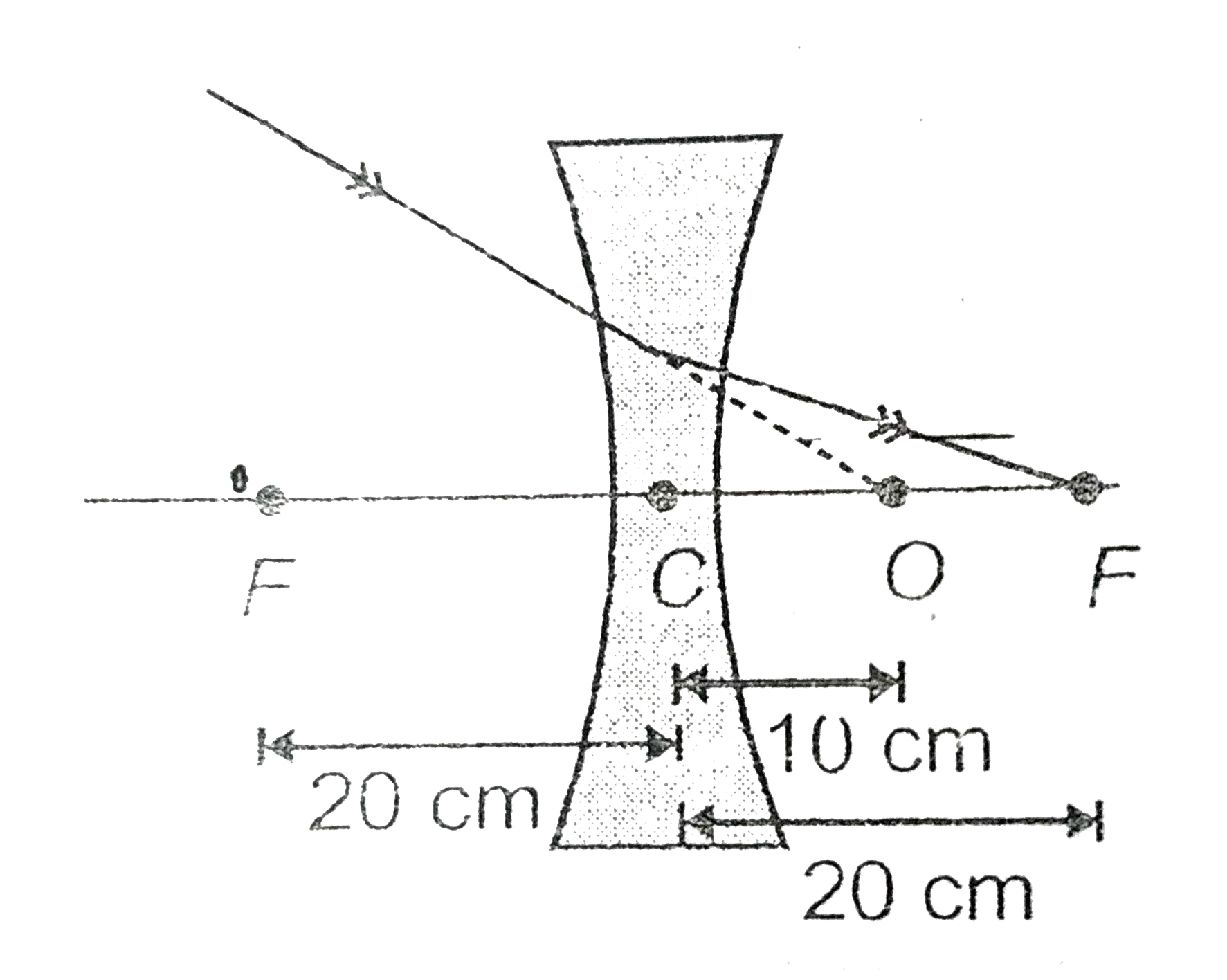
A converging beam of light is incident on a concave lens of focal length 20 cm. In the absence of the lens, the beam converges at a point 10 m behind the lens. Find where the beam will converge/diverge after refraction.

Video Solution

Text Solution

Verified by Experts

The situation is shown. O is the virtual object
u = + 10 cm
f = -20 cm
$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$
$\frac{1}{v} = \frac{1}{u} + \frac{1}{f} = \frac{1}{10} - \frac{1}{20} = \frac{1}{20}$
$\Rightarrow v = + 20 c m$ . The beam converges at a point 20 cm behind the lens.

Updated on:21/07/2023

If a converging beam of light is incident on a concave mirror, the reflected light
AMay form a real image
BMust form a real image
CMay form a virtual image
DMay be a parallel beam
A convergent beam is incident on a convex mirror. Reflected light
Amay form a real image
Bmay form a virtual image
Cmust form a real image
Dmust form a virtual image
A converging beam of light is incident on a concave lens. The beam converges behind the lens at 15 cm from its centre, in the absence of the lens. Select the correct alternative
AAfter passing through the lens, beam becomes diverging, what ever may be the focal length
BIf focal length = 10 cm, the beam diverges away
CIf focal length = 20 cm, the beam diverges away
DFocal length = 30 cm, beam converged at focal point of the lens