The figure shows top view of a conducting rob AB, bent to form a semicircle of radius R, carrying current I, placed on a smooth horizontal table. It is subjected to a uniform magnetic field B perpendicular to its plane as shown. The rod is held at rest in its position by two light strings attached to its ends. Calculate the magnetic force acting on the conductor AB and the tension in the strings.
Strategy: To find the force conductor, consider a small arc of length dl=Rdθ. This arc can be consider as a straight conductor of length dl.
To solve the problem of calculating the magnetic force acting on the conductor AB and the tension in the strings, we can follow these steps:
1. Understanding the Setup:
- We have a conducting rod AB bent into a semicircle of radius R carrying a current I.
- The rod is placed on a smooth horizontal table and is subjected to a uniform magnetic field B that is perpendicular to its plane.
2. Magnetic Force on a Small Element:
- The magnetic force dF on a small element of the rod can be calculated using the formula:
dF=Idl×B
- Here, dl is the length of the small element of the rod.
3. Expressing dl:
- For a small angle dθ subtended at the center of the semicircle, the length of the small arc dl can be expressed as:
dl=Rdθ
4. Calculating the Force:
- Substituting dl into the expression for dF:
dF=I(Rdθ)×B
- The direction of dF will depend on the angle θ.
5. Integrating to Find Total Force:
- The total force F acting on the entire semicircular rod can be found by integrating dF from θ=0 to θ=π:
F=∫π0dF=∫π0I(Rdθ)×Bsin(θ)
- Since B is constant, we can factor it out:
F=IRB∫π0sin(θ)dθ
6. Evaluating the Integral:
- The integral ∫π0sin(θ)dθ=2:
F=IRB⋅2=2IRB
7. Finding the Tension in the Strings:
- The net force F acting on the rod must be balanced by the tension T in the strings. Since there are two strings, we have:
F=2T
- Substituting the expression for F:
2IRB=2T
- Therefore, the tension in each string is:
T=IRB
Final Answers:
- The magnetic force acting on the conductor AB is F=2IRB.
- The tension in the strings is T=IRB.
- We have a conducting rod AB bent into a semicircle of radius R carrying a current I.
- The rod is placed on a smooth horizontal table and is subjected to a uniform magnetic field B that is perpendicular to its plane.
- The magnetic force dF on a small element of the rod can be calculated using the formula:
dF=Idl×B
- Here, dl is the length of the small element of the rod.
- For a small angle dθ subtended at the center of the semicircle, the length of the small arc dl can be expressed as:
dl=Rdθ
- Substituting dl into the expression for dF:
dF=I(Rdθ)×B
- The direction of dF will depend on the angle θ.
- The total force F acting on the entire semicircular rod can be found by integrating dF from θ=0 to θ=π:
F=∫π0dF=∫π0I(Rdθ)×Bsin(θ)
- Since B is constant, we can factor it out:
F=IRB∫π0sin(θ)dθ
- The integral ∫π0sin(θ)dθ=2:
F=IRB⋅2=2IRB
- The net force F acting on the rod must be balanced by the tension T in the strings. Since there are two strings, we have:
F=2T
- Substituting the expression for F:
2IRB=2T
- Therefore, the tension in each string is:
T=IRB
- The magnetic force acting on the conductor AB is F=2IRB.
- The tension in the strings is T=IRB.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Illustration
14 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Try Yourself
27 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Knowledge Check
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
What is the force experienced by a semicircular wire of radius R when it is carrying a current l and is placed in a uniform magnetic field of induction B as shown in figure. ?
View SolutionFigure shows an equilateral triangle ABC of side l carrying currents as shown, and placed in a uniform magnetic field B perpendicular to the plane of triangle. The magnitude of magnetic force on the triangle is

View SolutionFigure shows an equilateral triangle ABC of side l carrying currents as shown, and placed in a uniform magnetic field B perpendicular to the plane of triangle. The magnitude of magnetic force on the triangle is

View SolutionA conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to

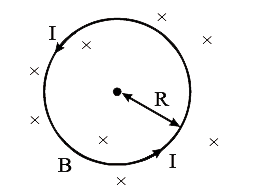
View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View SolutionA current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
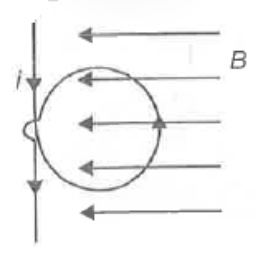
View SolutionAs shown in diagram, a current carrying conductor is subjected to steady uniform magnetic field. Then
View Solution
