Find the magnetic field at the ccentre of a current carrying conductor bent in the form of an arc subtending angle θ at its centre. Radius of the arc is R
Strategy: Let the arc lie in x-y plane with its centre at the origin. Consider a small current element i→dl as shown. The field due to this element at the centre can be obtained by Biot-Savart law
To find the magnetic field at the center of a current-carrying conductor bent in the form of an arc subtending an angle θ at its center with a radius R, we can follow these steps:
1. Understanding the Setup:
- We have a current-carrying arc of radius R that subtends an angle θ at the center. The arc lies in the x-y plane with its center at the origin.
2. Applying the Biot-Savart Law:
- According to the Biot-Savart law, the magnetic field dB due to a small current element idl at a distance R from the center is given by:
dB=μ04πidlsinϕR2
- Here, ϕ is the angle between the current element dl and the line connecting the element to the point where the field is being calculated (the center of the arc).
3. Determining dl:
- For an arc, the length of the current element dl can be expressed in terms of the angle dϕ:
dl=Rdϕ
4. Substituting into the Biot-Savart Law:
- Since the angle ϕ is 90∘ (as dl is perpendicular to the radius at the center), we have sinϕ=1:
dB=μ04πiRdϕR2=μ0i4πRdϕ
5. Integrating to Find Total Magnetic Field:
- To find the total magnetic field B at the center, we integrate dB from 0 to θ:
B=∫θ0dB=∫θ0μ0i4πRdϕ
- This simplifies to:
B=μ0i4πR∫θ0dϕ=μ0i4πR(ϕ)θ0=μ0i4πRθ
6. Final Result:
- Therefore, the magnetic field at the center of the arc is:
B=μ0iθ4πR
- We have a current-carrying arc of radius R that subtends an angle θ at the center. The arc lies in the x-y plane with its center at the origin.
- According to the Biot-Savart law, the magnetic field dB due to a small current element idl at a distance R from the center is given by:
dB=μ04πidlsinϕR2
- Here, ϕ is the angle between the current element dl and the line connecting the element to the point where the field is being calculated (the center of the arc).
- For an arc, the length of the current element dl can be expressed in terms of the angle dϕ:
dl=Rdϕ
- Since the angle ϕ is 90∘ (as dl is perpendicular to the radius at the center), we have sinϕ=1:
dB=μ04πiRdϕR2=μ0i4πRdϕ
- To find the total magnetic field B at the center, we integrate dB from 0 to θ:
B=∫θ0dB=∫θ0μ0i4πRdϕ
- This simplifies to:
B=μ0i4πR∫θ0dϕ=μ0i4πR(ϕ)θ0=μ0i4πRθ
- Therefore, the magnetic field at the center of the arc is:
B=μ0iθ4πR
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Illustration14videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Try Yourself27videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D16videos
MOVING CHARGE AND MAGNESIUM
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
Similar Questions
The magnetic field at the centre of the current carrying coil is
View SolutionFind magnetic field at O due to the current carrying conductor as shown in the figure.
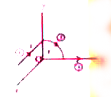 View Solution
View SolutionFind the magnetic field at centre P due to current i in the conductor as shown in fig.
 View Solution
View SolutionThe magnetic field at centre O of the arc in Fig.
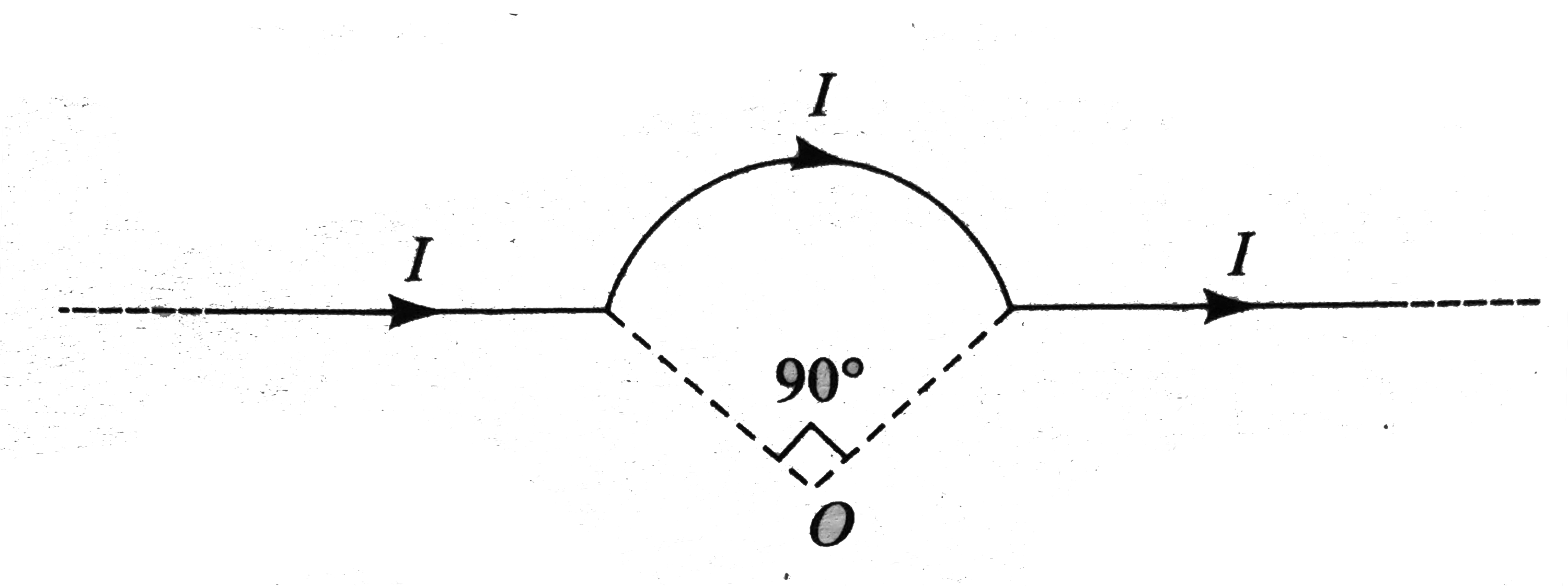 View Solution
View SolutionWhat will be magnetic field at centre of current carrying circular loop of radius R?
View SolutionRatio of magnetic field at the centre of a current carrying coil of radius R and at a distance of 3R on its axis is
View SolutionThe magnetic field at centre of a hexagonal coil of side l carrying a current I is
 View Solution
View SolutionA piece of wire 20 cm long is bent into the form of an arc of a circle, subtending an angle of 60∘ at its centre. Find the radius of the circle.
View SolutionThe magnetic field at the origin due to a current element I (→dl)placedataposi→n(→r)is
View SolutionThe ratio of the magnetic field at the centre of a current carrying circular coil to its magnetic moment is x. If the current and radius both are doubled the new ratio will become
View Solution
