A current carrying conductor of length l is bent into two loops one by one. First loop has one turn of wire and the second loop has two turns of wire. Compare the magnetic fields at the centre of the loops
To compare the magnetic fields at the center of two loops formed by a current-carrying conductor of length L, we can follow these steps:
Step 1: Determine the radius of the first loop
For the first loop, which has one turn, the circumference is equal to the length of the wire:
2πr1=L
From this, we can solve for the radius r1:
r1=L2π
Step 2: Calculate the magnetic field at the center of the first loop
The magnetic field B1 at the center of a single loop carrying current I is given by the formula:
B1=μ0I2r1
Substituting r1 from Step 1:
B1=μ0I2(L2π)=μ0I⋅πL
Step 3: Determine the radius of the second loop
For the second loop, which has two turns, the total length of the wire is still L, but the circumference is now:
2×2πr2=L
From this, we can solve for the radius r2:
4πr2=L⟹r2=L4π=r12
Step 4: Calculate the magnetic field at the center of the second loop
The magnetic field B2 at the center of the second loop, also carrying the same current I, is given by:
B2=μ0I2r2
Substituting r2 from Step 3:
B2=μ0I2(L4π)=μ0I⋅2πL
Step 5: Compare the magnetic fields B1 and B2
Now we can compare B2 with B1:
B2=μ0I⋅2πL=2(μ0I⋅πL)=2B1
Thus, we conclude that:
B2=2B1
Final Conclusion
The magnetic field at the center of the second loop (with two turns) is twice that of the magnetic field at the center of the first loop (with one turn).
---
For the first loop, which has one turn, the circumference is equal to the length of the wire:
2πr1=L
From this, we can solve for the radius r1:
r1=L2π
The magnetic field B1 at the center of a single loop carrying current I is given by the formula:
B1=μ0I2r1
Substituting r1 from Step 1:
B1=μ0I2(L2π)=μ0I⋅πL
For the second loop, which has two turns, the total length of the wire is still L, but the circumference is now:
2×2πr2=L
From this, we can solve for the radius r2:
4πr2=L⟹r2=L4π=r12
The magnetic field B2 at the center of the second loop, also carrying the same current I, is given by:
B2=μ0I2r2
Substituting r2 from Step 3:
B2=μ0I2(L4π)=μ0I⋅2πL
Now we can compare B2 with B1:
B2=μ0I⋅2πL=2(μ0I⋅πL)=2B1
Thus, we conclude that:
B2=2B1
The magnetic field at the center of the second loop (with two turns) is twice that of the magnetic field at the center of the first loop (with one turn).
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Illustration14videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Try Yourself27videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D16videos
MOVING CHARGE AND MAGNESIUM
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
Similar Questions
A square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionThe wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,
 View Solution
View SolutionA current I flows along a triangle loop having sides of equal length a. The strength of magnetic field at the centre of the loop is :
 View Solution
View SolutionA current I is flowing in a conductor of length L when it is bent in the form of a circular loop its magnetic moment
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is (dependence on L)
View SolutionA conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.
 View Solution
View SolutionOne of the two identical conducting wires of length L is bent in the form of a circular loop and the other one into a circular coil of N identical turns. If the same current passed in both, the ratio of the magnetic field at the central of the loop (BL) to that at the central of the coil (BC), i.e. BLBC will be :
View SolutionAn infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R metre. The magnetic induction at the centre of loop is
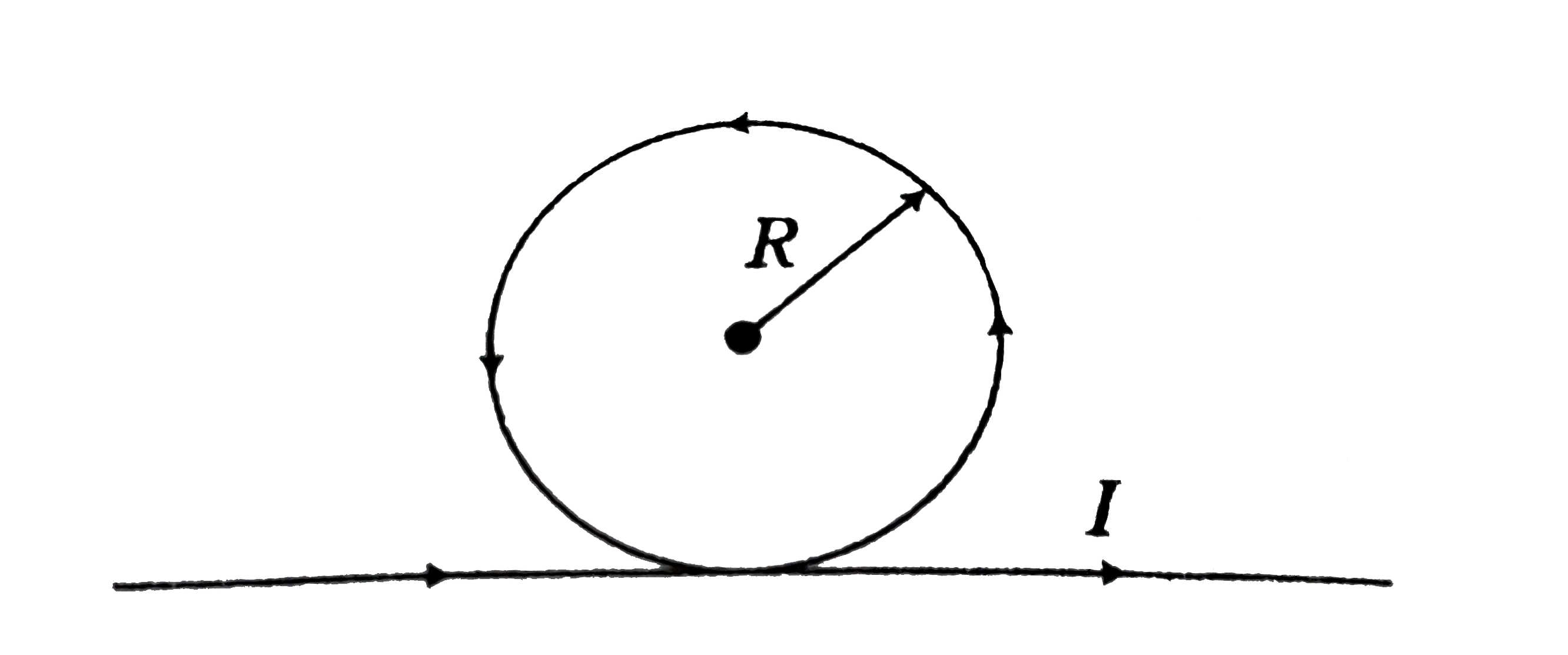 View Solution
View Solution
