An 850 W consumer coffee maker can make 10 cups (1.75 litres) of 80∘C coffee from 20∘C tap water in 10 minutes. What percentage of the electrical energy consumed actually makes it to the coffee?
To solve the problem, we need to calculate the percentage of electrical energy consumed by the coffee maker that actually goes into heating the coffee. We will follow these steps:
Step 1: Calculate the heat required to raise the temperature of water
We use the formula for heat energy required:
Q=mcΔT
Where:
- m = mass of the water
- c = specific heat capacity of water
- ΔT = change in temperature
Given:
- Volume of water = 1.75 liters = 1.75 kg (since the density of water is approximately 1000kg/m3)
- Specific heat capacity of water, c=4200J/(kg°C)
- Initial temperature, Ti=20°C
- Final temperature, Tf=80°C
- Change in temperature, ΔT=Tf−Ti=80−20=60°C
Calculation:
Q=1.75kg×4200J/(kg°C)×60°C
Q=1.75×4200×60=441000J
Step 2: Calculate the electrical energy consumed by the coffee maker
The electrical energy consumed can be calculated using the formula:
W=P×t
Where:
- P = power of the coffee maker (in watts)
- t = time (in seconds)
Given:
- Power, P=850W
- Time, t=10minutes=10×60=600seconds
Calculation:
W=850W×600s=510000J
Step 3: Calculate the efficiency of the coffee maker
The efficiency can be calculated using the formula:
Efficiency=(QW)×100%
Calculation:
Efficiency=(441000J510000J)×100%
Efficiency=(0.865)×100%=86.5%
Final Answer:
The percentage of the electrical energy consumed that actually makes it to the coffee is 86.5%.
---
Q=mcΔT
Where:
- m = mass of the water
- c = specific heat capacity of water
- ΔT = change in temperature
- Volume of water = 1.75 liters = 1.75 kg (since the density of water is approximately 1000kg/m3)
- Specific heat capacity of water, c=4200J/(kg°C)
- Initial temperature, Ti=20°C
- Final temperature, Tf=80°C
- Change in temperature, ΔT=Tf−Ti=80−20=60°C
Q=1.75kg×4200J/(kg°C)×60°C
Q=1.75×4200×60=441000J
W=P×t
Where:
- P = power of the coffee maker (in watts)
- t = time (in seconds)
- Power, P=850W
- Time, t=10minutes=10×60=600seconds
W=850W×600s=510000J
Efficiency=(QW)×100%
Efficiency=(441000J510000J)×100%
Efficiency=(0.865)×100%=86.5%
The percentage of the electrical energy consumed that actually makes it to the coffee is 86.5%.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:AAKASH INSTITUTE ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Try Youself
Explore 16 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH INSTITUTE ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Assignment (Section-A) Objective Type questions (one option is correct)
Explore 50 Videos
- TEST2Book:AAKASH INSTITUTE ENGLISHChapter:TEST2Exercise:EXERCISE
Explore 2 Videos
- THERMODYNAMICSBook:AAKASH INSTITUTE ENGLISHChapter:THERMODYNAMICSExercise:ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
Explore 10 Videos
Similar Questions
An incandescent lamp consumint P=54W is immersed into a transparent calorimeter containing V=103cm3 of water in 420 s the water is heated by 4∘C. The percentage of the energy consumed by the lamp that passes out of the calorimeter in the form of radiant energy is
View SolutionAn electric kettle taking 3Aat210V brings 1L of water from 20∘C→80∘Cin10min. Find its efficiency.
View SolutionA heating coil of 2000W is immersed in water . How much time will it take in raising the temperature of 1L of water from 4∘Cto100∘C? Only 80% of the thermal energy produced is used in raising the temperature of water.
View SolutionA 1kW heater is meant to operate at 200V.
(a) What is the resistance?
(b) How much power will it consume if the line voltage drops to 100V?
( c ) How many units of electrical energy will it consume in a month (of30days) if it operates 10hdaily at the specified voltage (200V)?
View SolutionA carbot freezer takes heat from water at 0∘C inside it and rejects it to the room at a temperature of 27∘C. The latent heat of ice is 336×103Jkg−1. If 5kg of water at 0∘C is converted into ice at 0∘C by the freezer, then the energy consumed by the freezer is close to :
View SolutionAluminium container of mass of 10 g contains 200 g of ice at−20∘C. Heat is added to the system at the rate of 100 calories per second. What is the temperature of the system after four minutes? Draw a rough sketch showing the variation of the temperature of the system as a function of time . Given:
Specific heat of ice = 0.5calg−1(.∘C)−1
Specific heat of aluminium = 0.2calg−1(.∘C)−1
Latent heat of fusion of ice = 80calg−1
View SolutionA single conservative force F(x) acts on a on a (1.0kg ) particle that moves along the x-axis. The potential energy U(x) is given by:
U(x)=20+(x−2)2
where, x is meters. At x=5.0m the particle has a kinetic energy of 20J
(a) What is the mechanical energy of the system?
(b) Make a plot of U(x) as a function of x for −10m≤x≤10m, and on the same graph draw the line that represents the mechanical energy of the system. Use part (b) to determine.
(c) The least value of x and
(d) the greatest value of x between which the particle can move.
(e) The maximum kinetic energy of the particle and
(f) the value of x at which it occurs.
(g) Datermine the equation for F(x) as a function of x.
(h) For what (finite ) value of x does F(x)=0?.
View SolutionLiquid water coats an active (growing) icicle and extends up a short, narrow tube along the central axis. Because the water-ice interface must have a temperature of 0∘C, the water in the tube cannot lose energy through the sides of the icicle or down through the tip because there is no temperature change in those directions . It can lose energy and freeze only by sending energy up(through distance L) to the top of the icicle, where the temperature Tr can be below 0∘C. Take L=0.10m and Tr=−5∘C.Assume that the central tube and the upward conduction path both have crosse-sectional area A=0.5m2. The thermal conductivity of ice is 0.40 W/m⋅K, latent heat of fusion is LF=4.0×105J/K and the density of liquid water is 1000 kg/m3.
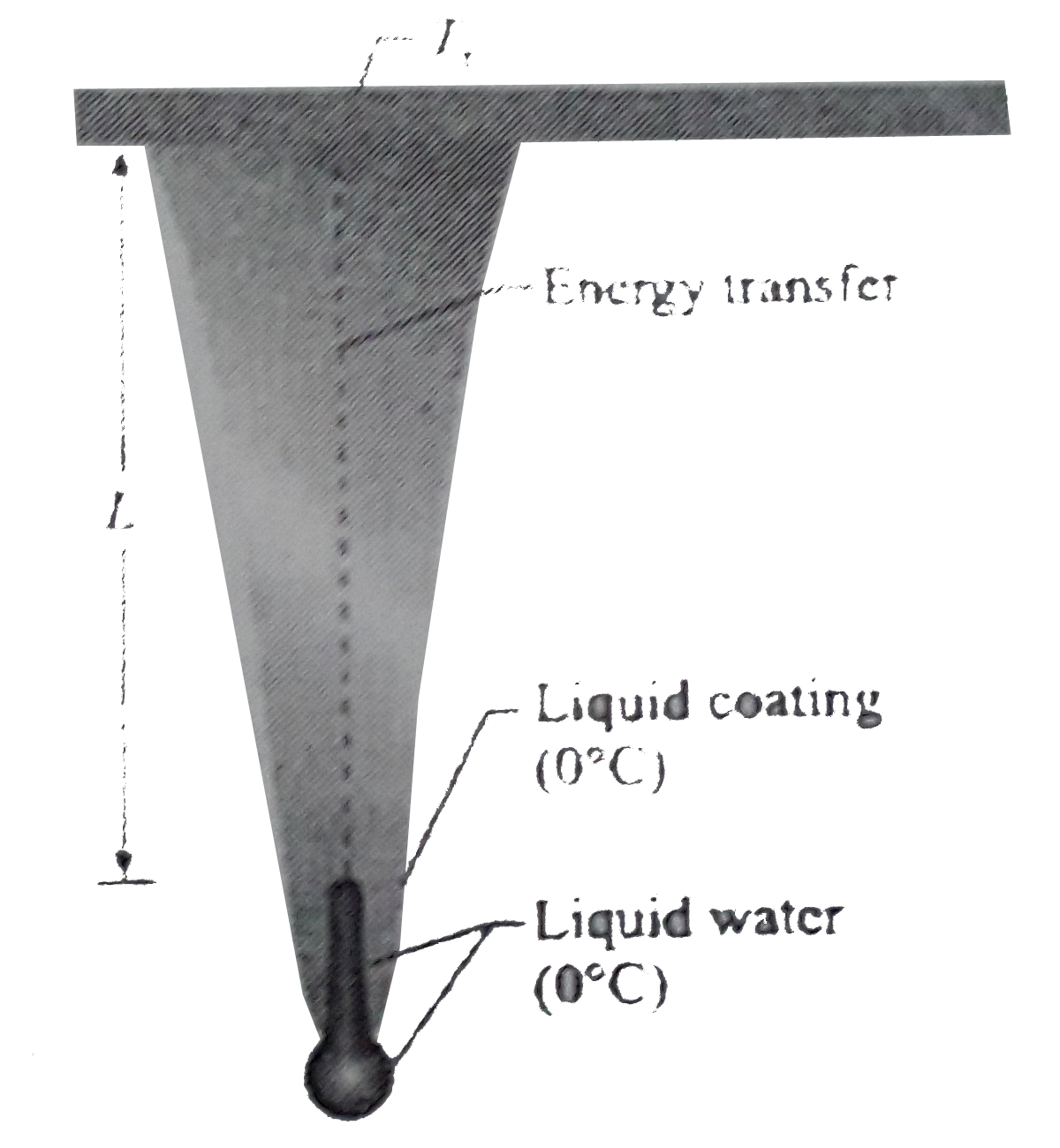
At what rate does the top of the tube move downward because of water freezing there?
View SolutionLiquid water coats an active (growing) icicle and extends up a short, narrow tube along the central axis. Because the water-ice interface must have a temperature of 0∘C, the water in the tube cannot lose energy through the sides of the icicle or down through the tip because there is no temperature change in those directions . It can lose energy and freeze only by sending energy up(through distance L) to the top of the icicle, where the temperature Tr can be below 0∘C. Take L=0.10m and Tr=−5∘C.Assume that the central tube and the upward conduction path both have crosse-sectional area A=0.5m2. The thermal conductivity of ice is 0.40 W/m⋅K, latent heat of fusion is LF=4.0×105J/K and the density of liquid water is 1000 kg/m3.
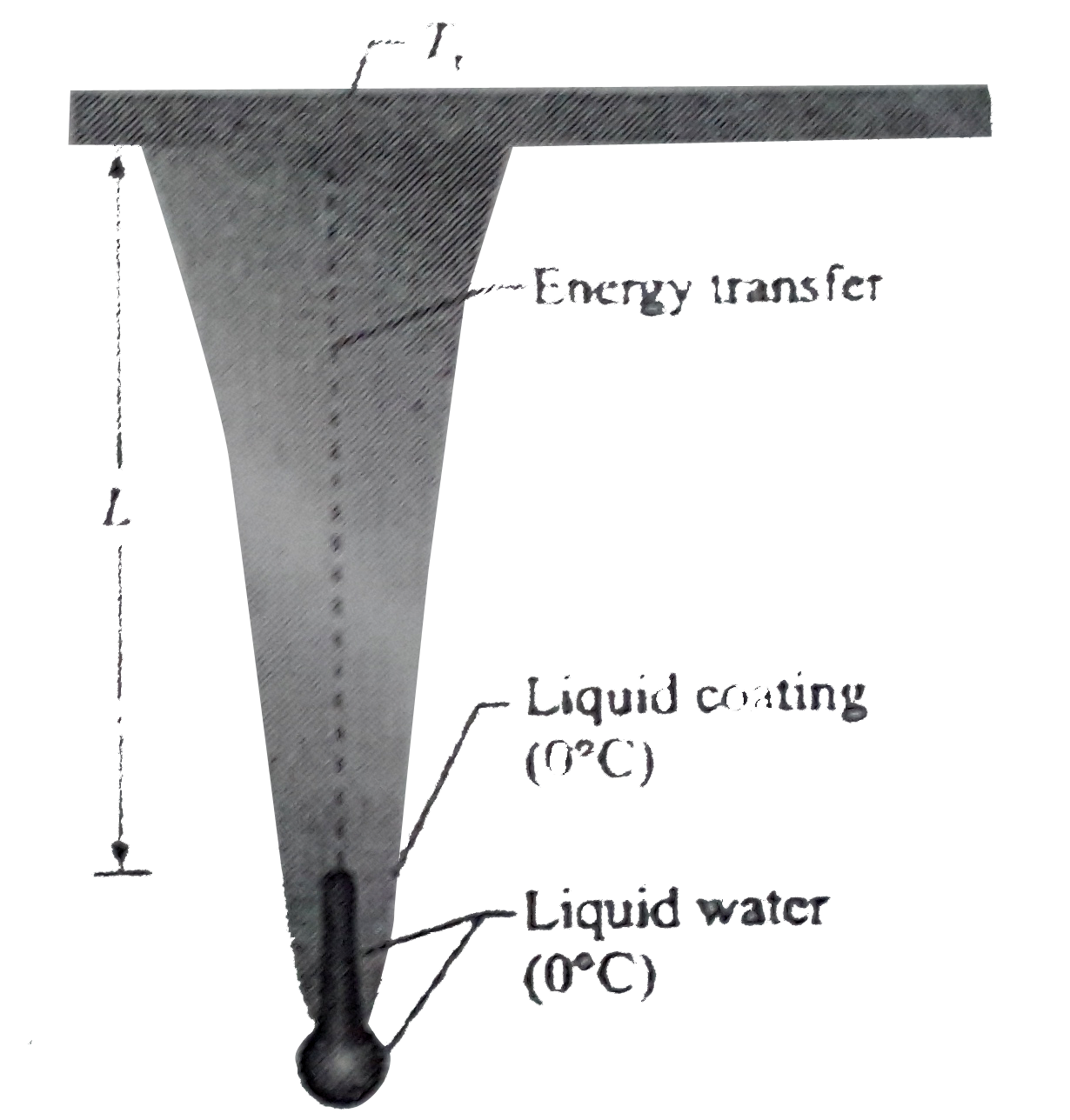
The rate at which mass converted from liquid to ice at the top of the central tube is
View Solution5 mole of oxygen are heated at constant volume from 10∘Cto20∘C. What will be the change in internal energy of the gas? Gram molar specific heat of gas at constant pressure =8cal.Mole−1.∘C−1 and R=8.36Jmole−1.∘C−1.
View Solution
