If force constant = 100 N/m, find the potential energy of the block at 0.05 m from the mean position
Hint :P.E.=12kx2
To find the potential energy of the block at a distance of 0.05 m from the mean position, we can use the formula for potential energy in a spring system:
Step 1: Write down the formula for potential energy (P.E.)
The potential energy (P.E.) stored in a spring is given by the formula:
P.E.=12kx2
where k is the force constant (spring constant) and x is the displacement from the mean position.
Step 2: Substitute the values into the formula
Given:
- Force constant k=100N/m
- Displacement x=0.05m
Now substituting these values into the formula:
P.E.=12×100×(0.05)2
Step 3: Calculate (0.05)2
Calculating (0.05)2:
(0.05)2=0.0025
Step 4: Substitute (0.05)2 back into the equation
Now substituting 0.0025 back into the potential energy equation:
P.E.=12×100×0.0025
Step 5: Perform the multiplication
Calculating:
P.E.=12×100×0.0025=100×0.00252=0.252=0.125J
Step 6: Final answer
Thus, the potential energy of the block at 0.05 m from the mean position is:
P.E.=0.125J
---
The potential energy (P.E.) stored in a spring is given by the formula:
P.E.=12kx2
where k is the force constant (spring constant) and x is the displacement from the mean position.
Given:
- Force constant k=100N/m
- Displacement x=0.05m
P.E.=12×100×(0.05)2
Calculating (0.05)2:
(0.05)2=0.0025
Now substituting 0.0025 back into the potential energy equation:
P.E.=12×100×0.0025
Calculating:
P.E.=12×100×0.0025=100×0.00252=0.252=0.125J
Thus, the potential energy of the block at 0.05 m from the mean position is:
P.E.=0.125J
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION -A)
58 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION-B )
25 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)
13 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
For examples , find the potential energy of the block at 0.05 m from the mean position
View SolutionA block whose mass is 2 kg is fastened on a spring whose spring constant is 100 Nm−1 . It is pulled to a distance of 0.1 m from over a frictionless surface and is released at t=0. Calculate the kinetic eneryg of the block when it is 0.05 m away from its mean position.
View Solution
Knowledge Check
A block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 100N/m. the block is pulled to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. the kinetic energy and potential energy of the block when it is 5 cm away from the mean position is
A0.0375 J, 0.125 JB0.125 J, 0.375 JC0.125 J, 0.125 JD0.375 J, 0.375 J
Many builidings have other types of mass dampersas antisway devices ( Refers of Example 14) some like the Johns Honacock building in Boston,have a larger block oscillating at the end of spring and an a lubricated track. .Suppose the block has m=5.44×105kg and is designed to oscillate at a frequency of5√2 Hz and with amplitude xm=0.40m . Find the total mechanical energy E of the spring block system.
Hint :K=mω2=m(2πv)2
E=K+U=12mv2+12kx2
View SolutionIn SHM , potential energy of a particle at mean position is E1 and kinetic enregy is E2 , then
View SolutionA block of mass 2kg is connected with a spring of natural length 40cm of force constant K=200N/m. The cofficient of friction is μ=0.5. When released from the given position, acceleration of block will be

View SolutionForce acting on a particle is F=−8x in S.H.M. The amplitude of oscillation is 2 (in m) and mass of the particle is 0.5 kg. The total mechanical energy of the particle is 20 J. Find the potential energy of the particle in mean position (in J).
View SolutionIn the problem if k = 10 N/m, m=2kg, R=1m and A=2m. Find linear speed of the disc at mean position.
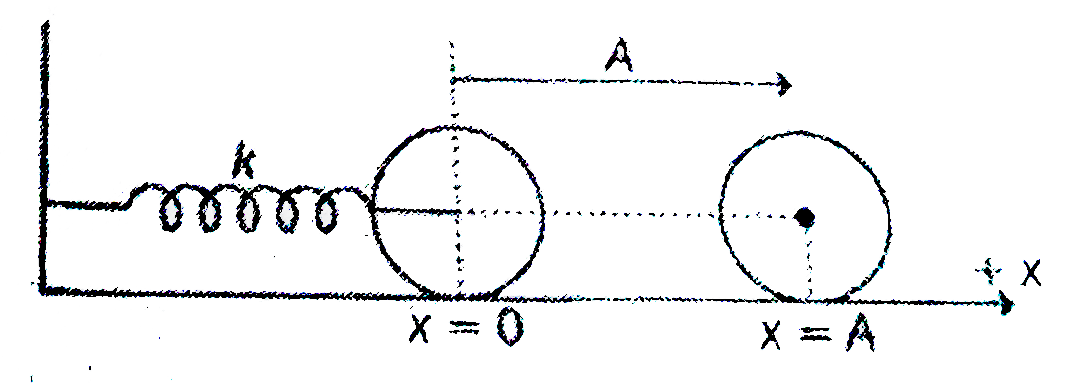
View SolutionA block B is pulled by a force of 18 N applied to a light pulley as shown in the figure. If the coefficient of friction is 0.4 and the acceleration of the block is 0.5 ms−2 , the mass of the block is (g=10m/s2)

View SolutionA spring mass systeam is shown in figure, spring is initially unstretched. A man starts pulling the block with constant force F. Find
(a) The amplitude and the time period of motion of the block
(b) The K.E. of the block at mean position
(c) The energy stored in the spring when the block passes through the mean position
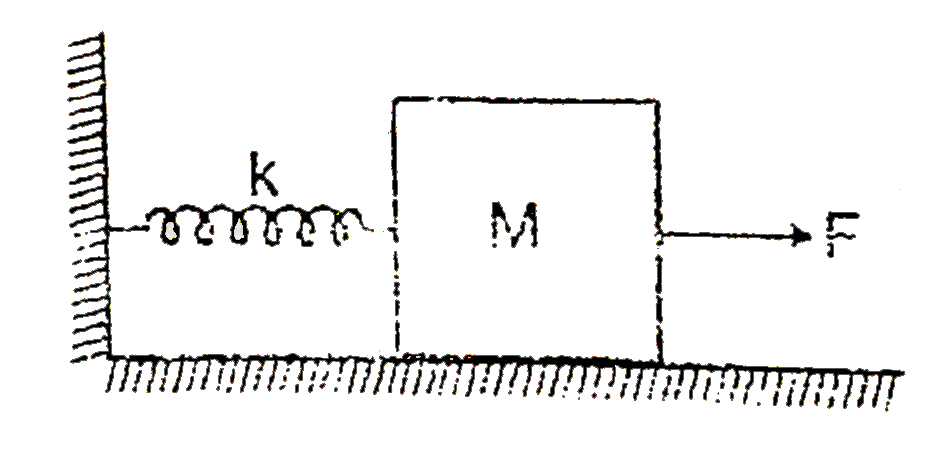
View Solution
