In SHM , potential energy of a particle at mean position is E1 and kinetic enregy is E2 , then
E1=E2
total potential energy at x=√3A2 is E1+3E24
total kinetic energy at x=√3A2 is 3E24
total kinetic energy at x=A√2 is E24
The correct Answer is:B
To solve the problem, we need to analyze the potential energy (U) and kinetic energy (K) of a particle in Simple Harmonic Motion (SHM) at the mean position.
1. Understanding SHM Energy Components:
- In SHM, the total mechanical energy (E) of the system is conserved and is the sum of kinetic energy (K) and potential energy (U).
- At the mean position (equilibrium position), the displacement (x) is zero.
2. Potential Energy at Mean Position:
- The potential energy (U) at the mean position is given as U=0 because potential energy in SHM is calculated using the formula U=12kx2 and at the mean position, x=0.
- Therefore, Umean=E1=0.
3. Kinetic Energy at Mean Position:
- The total energy (E) in SHM is given by E=K+U.
- Since U=0 at the mean position, the total energy is entirely kinetic.
- Thus, K=E at the mean position.
4. Maximum Kinetic Energy:
- The maximum kinetic energy (K_max) occurs at the mean position and is equal to the total energy of the system.
- Therefore, K=E2 at the mean position.
5. Conclusion:
- Given that E1=0 (potential energy at mean position) and E2=Kmax, we can conclude that the kinetic energy at the mean position is equal to the total energy of the system.
Final Answer:
- At the mean position, the potential energy E1=0 and the kinetic energy E2 is equal to the total energy of the system.
---
- In SHM, the total mechanical energy (E) of the system is conserved and is the sum of kinetic energy (K) and potential energy (U).
- At the mean position (equilibrium position), the displacement (x) is zero.
- The potential energy (U) at the mean position is given as U=0 because potential energy in SHM is calculated using the formula U=12kx2 and at the mean position, x=0.
- Therefore, Umean=E1=0.
- The total energy (E) in SHM is given by E=K+U.
- Since U=0 at the mean position, the total energy is entirely kinetic.
- Thus, K=E at the mean position.
- The maximum kinetic energy (K_max) occurs at the mean position and is equal to the total energy of the system.
- Therefore, K=E2 at the mean position.
- Given that E1=0 (potential energy at mean position) and E2=Kmax, we can conclude that the kinetic energy at the mean position is equal to the total energy of the system.
- At the mean position, the potential energy E1=0 and the kinetic energy E2 is equal to the total energy of the system.
Similar Questions
A particle is executing SHM with amplitude A. At displacement x=(−A4), force acting on the particle is F, potential energy of the particle is U, velocity of particle is v and kinetic energy is K. Assuming potential energyh to be zero at mean position. At displacement x=A/2
View SolutionKinetic energy of a particle on the surface is E0 and potential energy is−E02.
(a) Will the particle escape to infinity ?
(b) At some height its kinetic energy becomes 0.6E0. What is potential energy at this height ?
(c) If the particle escape to infinity , what is kinetic energy of the particle at infinity ?
View SolutionKinetic energy of a particle on the surface of earth is E0 and the potential energy is −2E0.
(a) Will the particle escape to infinity ?
(ii) What is the value of potential energy where speed of the particle becomes zero?
View SolutionPotential energy of a particle in SHM along x - axis is gives by
U=10+(x−2)2
Here, U is in joule and x in metre. Total mechanical energy of the particle is 26J. Mass of the particle is 2kg. Find
(a) angular frequency of SHM,
(b) potential energy and kinetic energy at mean position and extreme position,
(c ) amplitude of oscillation,
(d) x - coordinates between which particle oscillates.
View SolutionIn position A kinetic energy of a particle is 60 J and potential energy is -20 J. In position B, kinetic energy is 100 J and potential energy is 40 J. Then, in moving the particle from A to B
View SolutionA body is executing simple harmonic motion. At a displacement x (from its mean position) its potential energy is E1 and at a displacement y its potential energy is E2. The potential energy is E at displacement (x+y) . Then:
View SolutionThe ration of kinetic energy to the potential energy of a particle executing SHM at a distance equal to half its amplitude , the distance being measured from its equilibrium position is
View SolutionThe potential energy ‘V’ of a particle moving along the positive x-direction in a conservative force field varies as shown in the figure. The total energy is E=2. Draw the corresponding kinetic energy K vs x graph.
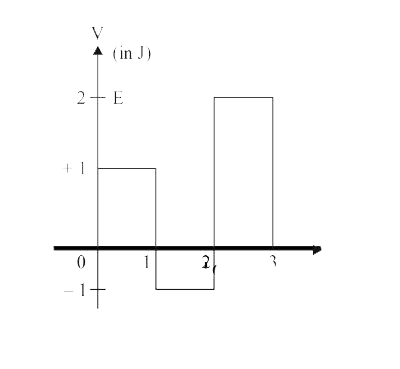
View SolutionPotential energy curve U of a particle as function of the position of a particle is shown. The particle has total mechanical energy E of 3.0 joules. Then select correct alternative.
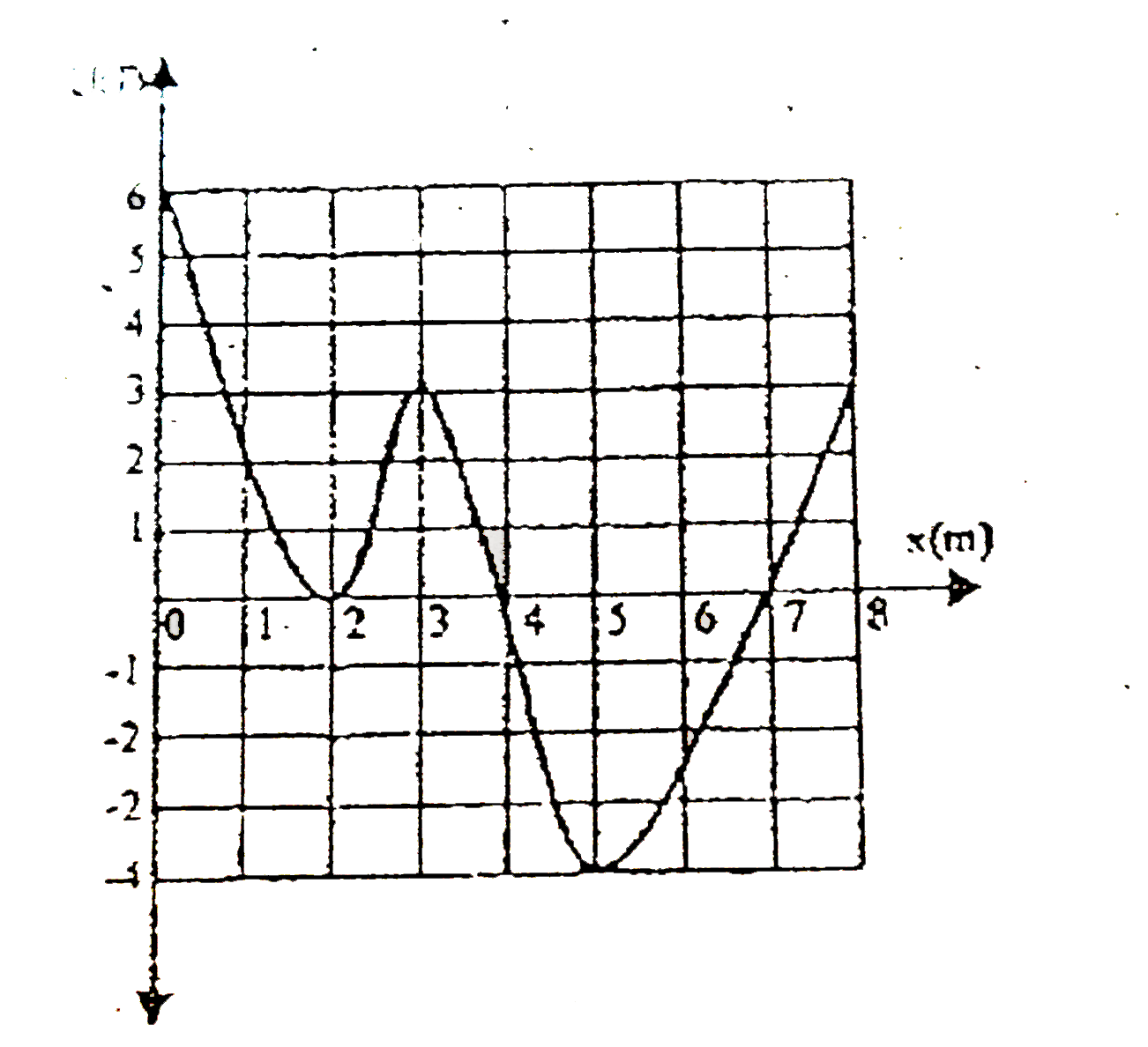
View SolutionIf A is amplitude of a particle in SHM, its displacement from the mean position when its kinetic energy is thrice that to its potential energy
View Solution
