A particle executes simple harmonic motion about x=0 along x-axis. The position of the particle at an instant is given by x=(5cm)sinπt. Find the average velocity and average acceleration for a time interval 0−0.5s.
Hint : Average velocity =x2−x1t2−t1
x1=5sin0
x2=5sin(π×0.5)
t2−t1=0.5
Average acceleration =v2−v1t2−t1
v=dxdt=5πcosπt
⇒aav=5πcos(π×0.5)−5πcosθ0.5
To solve the problem, we need to find the average velocity and average acceleration of a particle executing simple harmonic motion (SHM) given by the equation x=5sin(πt) over the time interval from t=0 to t=0.5 seconds.
Step 1: Calculate the positions at t=0 and t=0.5 seconds.
1. At t=0:
x1=5sin(π⋅0)=5sin(0)=0cm
2. At t=0.5:
x2=5sin(π⋅0.5)=5sin(π2)=5⋅1=5cm
Step 2: Calculate the average velocity.
The average velocity vavg is given by the formula:
vavg=x2−x1t2−t1
Substituting the values:
vavg=5cm−0cm0.5s−0s=5cm0.5s=10cm/s
Step 3: Calculate the velocity function.
To find the average acceleration, we first need the velocity function. The velocity v is the derivative of the position x with respect to time t:
v=dxdt=5πcos(πt)
Step 4: Calculate the velocities at t=0 and t=0.5 seconds.
1. At t=0:
v1=5πcos(π⋅0)=5πcos(0)=5π⋅1=5πcm/s
2. At t=0.5:
v2=5πcos(π⋅0.5)=5πcos(π2)=5π⋅0=0cm/s
Step 5: Calculate the average acceleration.
The average acceleration aavg is given by:
aavg=v2−v1t2−t1
Substituting the values:
aavg=0−5π0.5−0=−5π0.5=−10πcm/s2
Final Answers:
- Average Velocity: 10cm/s
- Average Acceleration: −10πcm/s2
---
x1=5sin(π⋅0)=5sin(0)=0cm
x2=5sin(π⋅0.5)=5sin(π2)=5⋅1=5cm
vavg=x2−x1t2−t1
vavg=5cm−0cm0.5s−0s=5cm0.5s=10cm/s
v=dxdt=5πcos(πt)
v1=5πcos(π⋅0)=5πcos(0)=5π⋅1=5πcm/s
v2=5πcos(π⋅0.5)=5πcos(π2)=5π⋅0=0cm/s
aavg=v2−v1t2−t1
aavg=0−5π0.5−0=−5π0.5=−10πcm/s2
- Average Velocity: 10cm/s
- Average Acceleration: −10πcm/s2
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION -A)58videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION-B )25videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)13videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)4videos
PHYSICAL WORLD
Similar Questions
A particle is executing SHM about y =0 along y-axis. Its position at an instant is given by y=(7m)sin(πt). Its average velocity for a time interval 0 to 0.5 s is
View SolutionPosition of a particle at any instant is given by x=3t2+1 , where x is in m and t in sec. Its average velocity in the time interval t=2 sec to t=3 sec will be :
View Solution
Knowledge Check
- Question 1 - Select One
A particle executing simple harmonic motion with an amplitude 5 cm and a time period 0.2 s. the velocity and acceleration of the particle when the displacement is 5 cm is
A0.5πms−1,0ms−2B0.5ms−1,−5π2ms−2C0ms−1,−5π2ms−2D0.5πms−1,−0.5π2ms−2
A particle moves along x-axis such that its position veries with time as x=50t−5t2. Select the correct alternative (s).
View SolutionA particle is moving along x-axis. The position of the particle at any instant is given by x=a+bt2, where, a=6mandb=3.5ms−2, t is measurved in seconds. Find.
Velocity of the particle at t = 0 and t = 3sView SolutionA particle is moving along x-axis. The position of the particle at any instant is given by x=a+bt2 where ,a= 6 m and b= 3.5 ms−2 't' is measured in second .Find
(i) the velocity of the particle at 1s and
(ii) the average velocity between 3s and 6sView SolutionThe position (x) of a particle moving along x - axis veries with time (t) as shown in figure. The average acceleration of particle in time interval t = 0 to t = 8 s is
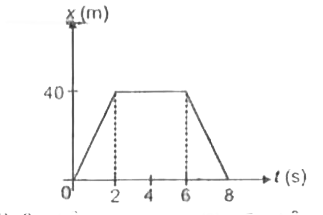 View Solution
View SolutionThe velocity of a particle are given by (4t–2) ms–1 along x–axis. Calculate the average acceleration of particle during the time interval from t = 1 to t = 2s.
View SolutionIf velocity of a particle is given by v=(2t+3)m/s. Then average velocity in interval 0≤t≤1 s is :
View SolutionThe position of a particle along X-axis at time t is given by x=2+t−3t2. The displacement and the distance travelled in the interval, t = 0 to t = 1 are respectively
View Solution
