A fixed spherical shell of inner radius R and outer radius 2R has mass M, A particle of mass m is held at rest at a distance 2R from the surface of the body. If the particle is released from that point, with what speed will it hit surface of the spherical body ?
To solve the problem step by step, we will use the principles of gravitational potential energy and conservation of energy.
1. Understanding the Setup:
- We have a spherical shell with an inner radius R and an outer radius 2R, and it has a mass M.
- A particle of mass m is held at rest at a distance 2R from the surface of the shell. Therefore, the total distance from the center of the shell to the particle is R+2R=3R.
2. Initial and Final Positions:
- The initial distance di between the mass m and the center of the shell is 3R.
- The final distance df when the particle hits the surface of the shell is 2R (the outer radius of the shell).
3. Using Conservation of Energy:
- The total mechanical energy is conserved. Thus, the initial potential energy plus the initial kinetic energy equals the final potential energy plus the final kinetic energy.
- Initial kinetic energy KEi=0 (since the particle is at rest).
- Final kinetic energy KEf=12mv2 (where v is the final speed we want to find).
- The gravitational potential energy U is given by U=−GMmr, where G is the gravitational constant, M is the mass of the shell, and r is the distance from the center of the shell.
4. Calculating Initial Potential Energy:
- The initial potential energy Ui when the particle is at a distance 3R is:
Ui=−GMm3R
5. Calculating Final Potential Energy:
- The final potential energy Uf when the particle hits the surface at a distance 2R is:
Uf=−GMm2R
6. Setting Up the Energy Conservation Equation:
- According to conservation of energy:
Ui+KEi=Uf+KEf
- Substituting the values:
−GMm3R+0=−GMm2R+12mv2
7. Simplifying the Equation:
- Rearranging gives:
12mv2=−GMm2R+GMm3R
- Finding a common denominator (6R):
12mv2=(−3GMm6R+2GMm6R)
12mv2=−GMm6R
8. Solving for v2:
- Cancel m from both sides (assuming m≠0):
12v2=GM6R
- Multiplying both sides by 2:
v2=GM3R
9. Finding v:
- Taking the square root:
v=√GM3R
Final Answer:
The speed with which the particle will hit the surface of the spherical body is:
v=√GM3R
- We have a spherical shell with an inner radius R and an outer radius 2R, and it has a mass M.
- A particle of mass m is held at rest at a distance 2R from the surface of the shell. Therefore, the total distance from the center of the shell to the particle is R+2R=3R.
- The initial distance di between the mass m and the center of the shell is 3R.
- The final distance df when the particle hits the surface of the shell is 2R (the outer radius of the shell).
- The total mechanical energy is conserved. Thus, the initial potential energy plus the initial kinetic energy equals the final potential energy plus the final kinetic energy.
- Initial kinetic energy KEi=0 (since the particle is at rest).
- Final kinetic energy KEf=12mv2 (where v is the final speed we want to find).
- The gravitational potential energy U is given by U=−GMmr, where G is the gravitational constant, M is the mass of the shell, and r is the distance from the center of the shell.
- The initial potential energy Ui when the particle is at a distance 3R is:
Ui=−GMm3R
- The final potential energy Uf when the particle hits the surface at a distance 2R is:
Uf=−GMm2R
- According to conservation of energy:
Ui+KEi=Uf+KEf
- Substituting the values:
−GMm3R+0=−GMm2R+12mv2
- Rearranging gives:
12mv2=−GMm2R+GMm3R
- Finding a common denominator (6R):
12mv2=(−3GMm6R+2GMm6R)
12mv2=−GMm6R
- Cancel m from both sides (assuming m≠0):
12v2=GM6R
- Multiplying both sides by 2:
v2=GM3R
- Taking the square root:
v=√GM3R
The speed with which the particle will hit the surface of the spherical body is:
v=√GM3R
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -J (Aakash Challengers Questions)
6 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - TRY YOUR SELF
33 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -H (Multiple True - False Type Questions)
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
A thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
View SolutionA particle of mass M is at a distance a from surface of a thin spherical shell of equal mass and having radius a.

View SolutionA particle of mass M is at a distance a from surface of a thin spherical shell of equal mass and having radius a.

View SolutionA solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole in the shell.
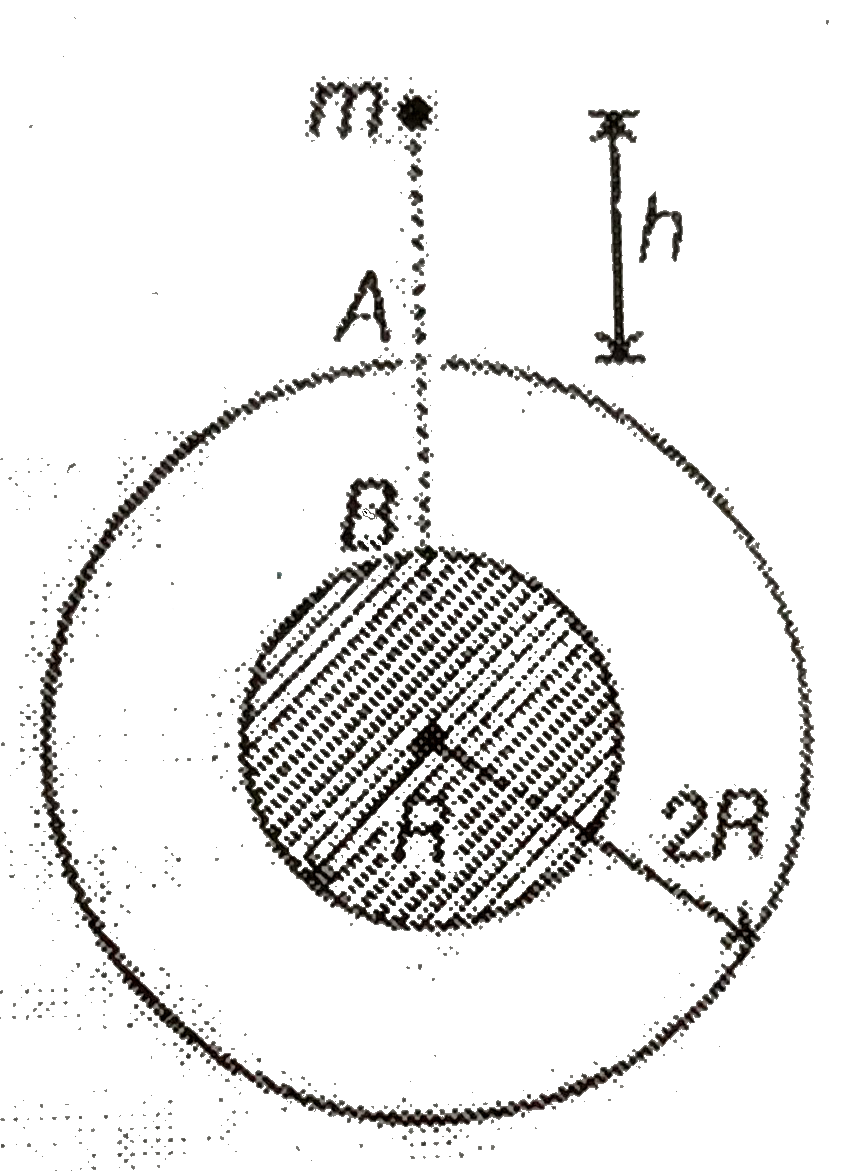
What speed will it collide at B?
View SolutionA metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is

View Solution_E01_069_Q01.png)
A solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole inn the shell.
QIn what time will it enter the hole at A
View SolutionA solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole in the shell.

What time will it take to move from A to B?
View SolutionA solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole in the shell.

At what time will it enter the hole at A
View SolutionA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View SolutionA spherical planet far out in space has mass 2M and radius a. A particle of mass m is falling freely near its surface. What will be the acceleration of that particle ?
View Solution
