Four point masses each mass m kept at the vertices of a square. A point mass m is kept at the point of intersection of the diagonal of a square. What be the force experienced by central mass m ?
The correct Answer is:Zero
To solve the problem of finding the force experienced by the central mass m placed at the intersection of the diagonals of a square formed by four point masses m at the vertices, we can follow these steps:
Step 1: Understand the Configuration
We have a square with four point masses m located at its vertices. The central mass m is placed at the intersection of the diagonals of the square.
Step 2: Determine the Distances
Let the side length of the square be a. The distance from each vertex to the center (intersection of the diagonals) can be calculated using the Pythagorean theorem. The distance r from a vertex to the center is given by:
r=a√2
Step 3: Calculate the Gravitational Force from Each Vertex
The gravitational force F exerted by each mass m at a distance r on the central mass m is given by Newton's law of gravitation:
F=Gm2r2
Substituting r=a√2:
F=Gm2(a√2)2=Gm2a22=2Gm2a2
Step 4: Analyze the Direction of Forces
Each of the four masses exerts a force on the central mass. The forces from the masses at opposite corners will have equal magnitudes but will act in opposite directions.
Step 5: Calculate the Net Force
Since the forces from the masses at opposite corners cancel each other out, we can analyze the forces in pairs:
1. The force from mass at (0,0) and (a,a) will cancel.
2. The force from mass at (0,a) and (a,0) will also cancel.
Thus, the net force Fnet on the central mass m is:
Fnet=0
Conclusion
The total force experienced by the central mass m is zero due to the symmetry of the configuration.
---
We have a square with four point masses m located at its vertices. The central mass m is placed at the intersection of the diagonals of the square.
Let the side length of the square be a. The distance from each vertex to the center (intersection of the diagonals) can be calculated using the Pythagorean theorem. The distance r from a vertex to the center is given by:
r=a√2
The gravitational force F exerted by each mass m at a distance r on the central mass m is given by Newton's law of gravitation:
F=Gm2r2
Substituting r=a√2:
F=Gm2(a√2)2=Gm2a22=2Gm2a2
Each of the four masses exerts a force on the central mass. The forces from the masses at opposite corners will have equal magnitudes but will act in opposite directions.
Since the forces from the masses at opposite corners cancel each other out, we can analyze the forces in pairs:
1. The force from mass at (0,0) and (a,a) will cancel.
2. The force from mass at (0,a) and (a,0) will also cancel.
Fnet=0
The total force experienced by the central mass m is zero due to the symmetry of the configuration.
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -A (Objective Type Questions (one option is correct))
50 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -B (Objective Type Questions (one option is correct))
20 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
Four particles each of mass m are kept at the four vertices of a square of side 'a' . Find gravitational potential energy of this system.
View SolutionThree point masses 'm' each are kept at three verties of a square pf side 'a' as shown in figure. Find gravitation potential and field strength at point O.
 .
.
View Solution
Knowledge Check
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−√2Gm2l(2−1√2)B−2Gm2l(2+1√2)C−√2Gm2l(√2−1√2)D−2Gm2l(√2−1√2)Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
AGm2l2[54+1√3]BGm2l2[34+1√3]CGm2l2[54−1√3]DGm2l2[34−1√3]
Four point masses each of mass m are placed on vertices of a regular tetrahedron. Distance between any two masses is r.
View SolutionSix point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
View SolutionFour equal masses (each of mass M) are placed at the corners of a square of side a. The escape velocity of a body from the centre O of the square is
View SolutionFour particles each of mass 'm' are placed at the four vertices of a square 'a' .Find net force on any one the particle.
View SolutionFour point masses are plaaced at four corners of a square as shows. When positions of mand 2m are interchanged

View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.
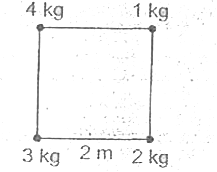
View Solution
