If the ring slips then will it be backward slipping or forward slipping.
To determine whether the ring will slip backward or forward, we need to analyze the conditions under which slipping occurs. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the System
We have a ring that is rotating and moving along a surface. The center of mass of the ring has a certain velocity (denoted as Vc), and there is a point of contact between the ring and the ground (denoted as point P).
Step 2: Identify the Conditions for Slipping
For the ring to be slipping, the velocity of the point of contact (point P) relative to the ground must not be zero. The ground is stationary, so the velocity of the ground (point Pg) is always zero.
Step 3: Analyze the Velocities
The velocity of point P can be expressed as:
Vp=Vc−rω
where:
- Vc is the velocity of the center of mass,
- r is the radius of the ring,
- ω is the angular velocity of the ring.
Step 4: Condition for Pure Rolling
For pure rolling (no slipping), the velocity of point P must equal the velocity of the ground:
Vp=0
This leads to the condition:
Vc=rω
Step 5: Determine Conditions for Forward and Backward Slipping
1. Forward Slipping: If the ring is slipping forward, the velocity of point P must be greater than zero:
Vp>0⟹Vc−rω>0⟹Vc>rω
This means the center of mass velocity is greater than the tangential velocity due to rotation.
2. Backward Slipping: If the ring is slipping backward, the velocity of point P must be less than zero:
Vp<0⟹Vc−rω<0⟹Vc<rω
This indicates that the center of mass velocity is less than the tangential velocity due to rotation.
Conclusion
- If Vc>rω, the ring is slipping forward.
- If Vc<rω, the ring is slipping backward.
We have a ring that is rotating and moving along a surface. The center of mass of the ring has a certain velocity (denoted as Vc), and there is a point of contact between the ring and the ground (denoted as point P).
For the ring to be slipping, the velocity of the point of contact (point P) relative to the ground must not be zero. The ground is stationary, so the velocity of the ground (point Pg) is always zero.
The velocity of point P can be expressed as:
Vp=Vc−rω
where:
- Vc is the velocity of the center of mass,
- r is the radius of the ring,
- ω is the angular velocity of the ring.
For pure rolling (no slipping), the velocity of point P must equal the velocity of the ground:
Vp=0
This leads to the condition:
Vc=rω
1. Forward Slipping: If the ring is slipping forward, the velocity of point P must be greater than zero:
Vp>0⟹Vc−rω>0⟹Vc>rω
This means the center of mass velocity is greater than the tangential velocity due to rotation.
Vp<0⟹Vc−rω<0⟹Vc<rω
This indicates that the center of mass velocity is less than the tangential velocity due to rotation.
- If Vc>rω, the ring is slipping forward.
- If Vc<rω, the ring is slipping backward.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - J) Aakash Challengers Questions
Explore 13 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:AAKASH INSTITUTE ENGLISHChapter:SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:Assignment (Section-D (Assertion and reason))
Explore 5 Videos
- TEST 1Book:AAKASH INSTITUTE ENGLISHChapter:TEST 1Exercise:EXERCISE
Explore 21 Videos
Similar Questions
The ratio of the accelerations for a solid sphere (mass m,andradiusR) rolling down an incline of angle θ without slipping, and slipping down the incline without rolling is
View SolutionA ladder placed on a smooth floor slips. If at a given instant the velocity with which the ladder is slipping on the floor is v1, and the velocity of that part of ladder which is touching the wall is v1, then the velocity of the centre of the ladder at that instant is:
View Solution
Knowledge Check
In the question number 82, the maximum permissible speed to avoid slipping is
A18.6ms−1B28.6ms−1C38.6ms−1D48.6ms−1
A uniform thin ring of mass 0.4kg rolls without slipping on a horizontal surface with a linear velocity of 10 cm/s. The kinetic energy of the ring is
View Solution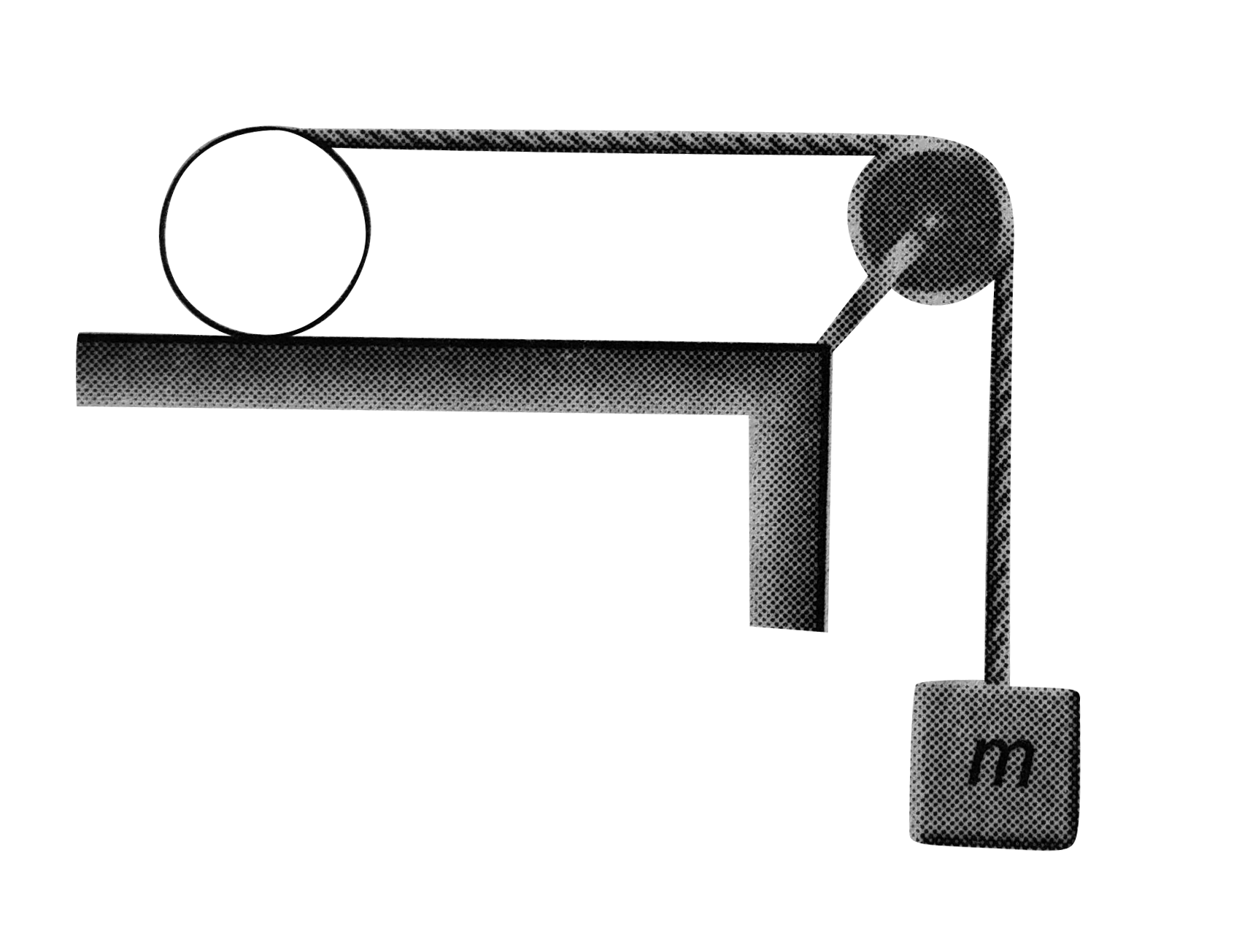
in the given figure a ring of mass m is kept on a horizontal surface while a body of equal mass m si attached through string, which is wounded on the ring. When the system is released the ring rolls without slipping. consider the following statement and choose the correct options.
(i). Acceleration of centre of mass of ring is 2g3
(ii). acceleration of hanging particle is 4g3
(iii). Frictional force (on the ring) acts in backward direction.
(iv) . Frictional force (on the ring) acts in backward direction.
View SolutionA ring, cylinder and solid sphere are placed on the top of a rough incline on which the sphere can just roll without slipping. When all of them are released at the same instant from the same position, then
View SolutionWe take 8 identical slips of paper, write the number 0 on one of them, the number 1 on three of the slips, the number 2 on three of the slips and the number 3 on one the ships. These slips are folded, put in a box and thoroughly mixed. One slip is drawn at random from the box. If X is the random variable denoting the number written on the drawn slip, find the probability distribution of X.
View SolutionA ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.



View SolutionTwo identical rings are moving with equal kinetic energy One ring rolls without slipping and other ring is in pure translational motion. The ratio of their respective speeds of centre of mass is
View SolutionA solid cylinder is attached to a horizonatal massless spring as shwn in figure.If the cyclinder rolls without slipping, the time period of oscillation of the cyclinder is

View Solution