A solid sphere and a hollow cylinder have the same radius and the same mass. They start from rest at the top of an incline. Which reaches the bottom first? Which has the greater speed at the bottom? Which has the greater total kinetic energy of the bottom ? Which has the greater rotational KE?
To solve the problem step by step, we will analyze each part of the question regarding the solid sphere and hollow cylinder.
Step 1: Moment of Inertia Calculation
1. Solid Sphere: The moment of inertia I for a solid sphere is given by:
Isphere=25mr2
2. Hollow Cylinder: The moment of inertia I for a hollow cylinder is given by:
Icylinder=mr2
Step 2: Determine Which Object Reaches the Bottom First
1. The acceleration a of an object rolling down an incline is given by:
a=g1+Imr2
2. Substitute the moment of inertia values:
- For the solid sphere:
asphere=g1+2/5mr2mr2=g1+25=g75=5g7
- For the hollow cylinder:
acylinder=g1+mr2mr2=g2
3. Since 5g7>g2, the solid sphere has greater acceleration and will reach the bottom first.
Step 3: Determine Which Object Has Greater Speed at the Bottom
1. The speed v at the bottom can be expressed as:
v=
⎷2gh⋅11+Imr2
2. Substitute the moment of inertia values:
- For the solid sphere:
vsphere=
⎷2gh⋅11+2/51=√2gh⋅57=√10gh7
- For the hollow cylinder:
vcylinder=√2gh⋅12=√gh
3. Since √10gh7>√gh, the solid sphere has a greater speed at the bottom.
Step 4: Determine Which Object Has Greater Total Kinetic Energy at the Bottom
1. The total kinetic energy KE at the bottom is given by:
KE=12mv2
2. Substitute the speed values:
- For the solid sphere:
KEsphere=12m⎛⎝√10gh7⎞⎠2=12m⋅10gh7=5mgh7
- For the hollow cylinder:
KEcylinder=12m(gh)=mgh2
3. Since 5mgh7>mgh2, the solid sphere has greater total kinetic energy at the bottom.
Step 5: Determine Which Object Has Greater Rotational Kinetic Energy
1. The rotational kinetic energy KErot is given by:
KErot=12Iω2
where ω=vr.
2. Substitute the moment of inertia values:
- For the solid sphere:
KErot,sphere=12⋅25mr2⋅(vspherer)2=12⋅25mr2⋅⎛⎜
⎜⎝√10gh7r⎞⎟
⎟⎠2=12⋅25m⋅10gh7=15m⋅10gh7=2mgh7
- For the hollow cylinder:
KErot,cylinder=12mr2⋅(vcylinderr)2=12mr2⋅(√ghr)2=12m⋅gh
3. Comparing the two:
- For the solid sphere: 2mgh7
- For the hollow cylinder: 12mgh or 3.5mgh7
4. Since 2mgh7<3.5mgh7, the hollow cylinder has greater rotational kinetic energy.
Summary of Answers:
1. Which reaches the bottom first? - Solid sphere
2. Which has the greater speed at the bottom? - Solid sphere
3. Which has the greater total kinetic energy at the bottom? - Solid sphere
4. Which has the greater rotational kinetic energy? - Hollow cylinder
1. Solid Sphere: The moment of inertia I for a solid sphere is given by:
Isphere=25mr2
2. Hollow Cylinder: The moment of inertia I for a hollow cylinder is given by:
Icylinder=mr2
1. The acceleration a of an object rolling down an incline is given by:
a=g1+Imr2
2. Substitute the moment of inertia values:
- For the solid sphere:
asphere=g1+2/5mr2mr2=g1+25=g75=5g7
- For the hollow cylinder:
acylinder=g1+mr2mr2=g2
3. Since 5g7>g2, the solid sphere has greater acceleration and will reach the bottom first.
1. The speed v at the bottom can be expressed as:
v=
⎷2gh⋅11+Imr2
2. Substitute the moment of inertia values:
- For the solid sphere:
vsphere=
⎷2gh⋅11+2/51=√2gh⋅57=√10gh7
- For the hollow cylinder:
vcylinder=√2gh⋅12=√gh
3. Since √10gh7>√gh, the solid sphere has a greater speed at the bottom.
1. The total kinetic energy KE at the bottom is given by:
KE=12mv2
2. Substitute the speed values:
- For the solid sphere:
KEsphere=12m⎛⎝√10gh7⎞⎠2=12m⋅10gh7=5mgh7
- For the hollow cylinder:
KEcylinder=12m(gh)=mgh2
3. Since 5mgh7>mgh2, the solid sphere has greater total kinetic energy at the bottom.
1. The rotational kinetic energy KErot is given by:
KErot=12Iω2
where ω=vr.
2. Substitute the moment of inertia values:
- For the solid sphere:
KErot,sphere=12⋅25mr2⋅(vspherer)2=12⋅25mr2⋅⎛⎜
⎜⎝√10gh7r⎞⎟
⎟⎠2=12⋅25m⋅10gh7=15m⋅10gh7=2mgh7
- For the hollow cylinder:
KErot,cylinder=12mr2⋅(vcylinderr)2=12mr2⋅(√ghr)2=12m⋅gh
3. Comparing the two:
- For the solid sphere: 2mgh7
- For the hollow cylinder: 12mgh or 3.5mgh7
4. Since 2mgh7<3.5mgh7, the hollow cylinder has greater rotational kinetic energy.
1. Which reaches the bottom first? - Solid sphere
2. Which has the greater speed at the bottom? - Solid sphere
3. Which has the greater total kinetic energy at the bottom? - Solid sphere
4. Which has the greater rotational kinetic energy? - Hollow cylinder
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - J) Aakash Challengers Questions
13 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
Which has greater reactivity
View SolutionA solid cylinder, a circular disc, a solid sphere and a hollow cylinder of the same radius are placed on an inclined plane. Which of the following will have maximum acceleration at the bottom of the plane?
View SolutionA solid cylinder and a hollow cylinder, both of the same mass and same external diameter are released from the same height at the same time on an inclined plane. Both roll down without slipping. Which one will reach the bottom first ?
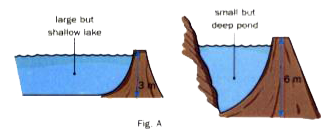
View SolutionA shallow lake and a deep pond are shown in Figure A. Which of them will have greater pressure at the bottom. Give reason.
View SolutionWhich of the following compounds has the greater dipole moment?
_E01_274_Q01.png)
View SolutionStatement 1: A solid sphere and a hollow sphere of same radius and same material are released (at rest ) from the top of a fixed inclined plane at the same time. They will reach the bottom simultaneously, if they roll with sliding.
Statement 2: In the situation of statement 1, the centres of both spheres have the same acceleration and they travel the same distance. Hence time taken is same.
View SolutionA hollow sphere and a solid sphere of the same dimensions rotate about the same axis with the same angular velocity. Which has greater kinetic energy ?
View SolutionA photon and an electron have the same de Broglie wavelength. Which has greater total energy? Explain
View SolutionA small steel sphere of mass m and radius r rolls without slipping on the fiictionless surface of a large hemisphere of radius R{R>>r) whose axis of symmetry is vertical. It starts at the top from the rest,
(a) What is the kinetic energy at the bottom ?
(b) What fraction is the rotational kinetic energy of the total kinetic energy ?
(c) What fraction is the rotational kinetic energy of the total kinetic energy?
(d) What fraction is the translational kinetic energy of the total kinetic energy?
View SolutionWhich of the following has ΔS∘ greater than zero
View Solution
