A bullet of mass 10 g moving with a velocity 300ms−1 strikes a wooden block and comes out from ot her side with a velocity of 200ms−1. Find the work done by t he resistive force on the bullet.
To find the work done by the resistive force on the bullet, we can use the concept of kinetic energy and the work-energy theorem. Here’s a step-by-step solution:
Step 1: Identify the given values
- Mass of the bullet, m=10g=10×10−3kg
- Initial velocity of the bullet, u=300m/s
- Final velocity of the bullet, v=200m/s
Step 2: Calculate the initial kinetic energy (KE_initial)
The formula for kinetic energy is given by:
KE=12mv2
Substituting the values for initial kinetic energy:
KEinitial=12×(10×10−3)×(300)2
Calculating this:
KEinitial=12×10−2×90000=0.5×900=450J
Step 3: Calculate the final kinetic energy (KE_final)
Now, we calculate the final kinetic energy using the same formula:
KEfinal=12mv2
Substituting the values for final kinetic energy:
KEfinal=12×(10×10−3)×(200)2
Calculating this:
KEfinal=12×10−2×40000=0.5×400=200J
Step 4: Calculate the change in kinetic energy
The change in kinetic energy (ΔKE) is given by:
ΔKE=KEfinal−KEinitial
Substituting the values:
ΔKE=200J−450J=−250J
Step 5: Work done by the resistive force
According to the work-energy theorem, the work done by the resistive force is equal to the change in kinetic energy:
W=ΔKE
Thus, the work done by the resistive force is:
W=−250J
Final Answer
The work done by the resistive force on the bullet is −250J.
---
- Mass of the bullet, m=10g=10×10−3kg
- Initial velocity of the bullet, u=300m/s
- Final velocity of the bullet, v=200m/s
The formula for kinetic energy is given by:
KE=12mv2
Substituting the values for initial kinetic energy:
KEinitial=12×(10×10−3)×(300)2
Calculating this:
KEinitial=12×10−2×90000=0.5×900=450J
Now, we calculate the final kinetic energy using the same formula:
KEfinal=12mv2
Substituting the values for final kinetic energy:
KEfinal=12×(10×10−3)×(200)2
Calculating this:
KEfinal=12×10−2×40000=0.5×400=200J
The change in kinetic energy (ΔKE) is given by:
ΔKE=KEfinal−KEinitial
Substituting the values:
ΔKE=200J−450J=−250J
According to the work-energy theorem, the work done by the resistive force is equal to the change in kinetic energy:
W=ΔKE
Thus, the work done by the resistive force is:
W=−250J
The work done by the resistive force on the bullet is −250J.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-A (OBJECTIVE TYPE QUESTIONS (ONE OPTIONISCORRECT)
60 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)
45 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION
2 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A bullet of mass 50 g moving with an initial velocity 100m s−1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate : Resistive force exerted by the wooden block.
View Solution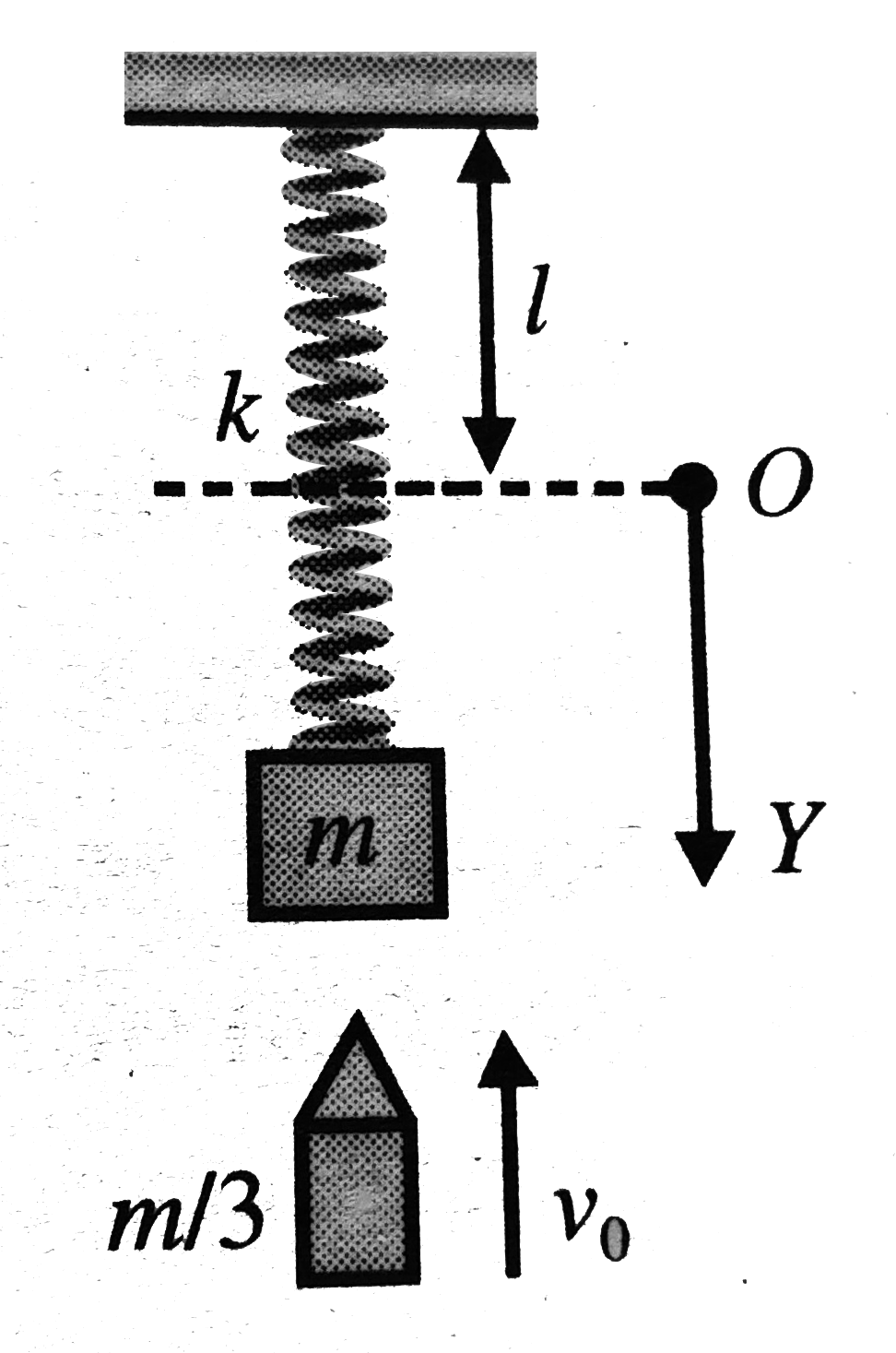
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The time taken by the block bullet system to move from y=mgk (initial equilibrium position) to y=0 (natural length of spring) is (A represents the amplitude of motion)
View SolutionA bullet of mass 50 g moving with an initial velocity 100m s−1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate : Retardation caused by the wooden block
View SolutionA bullet of mass 50 g moving with an initial velocity 100m s−1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate : Final momentum of the bullet
View SolutionA bullet of mass 50 g moving with an initial velocity 100m s−1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate : Initial momentum of the bullet
View SolutionA bullet of mass 0.04 kg moving with a speed of 90ms−1 enters a heavy wooden block and is stooped after a distance of 60 cm . What is the average resistive force exerted by the block on the bullet ?
View SolutionA bullet of mass 0.06 kg moving with a speed of 90ms−1 enters a heavy wooden block and it stopped after a distance of 60 cm. What is the average resistive force exerted by the block on the bullet ?
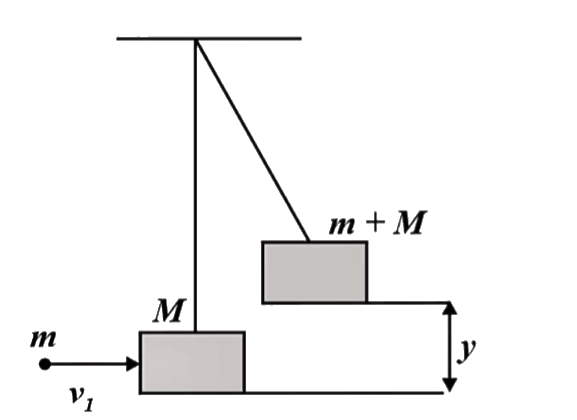
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
View SolutionA bullet of mass 10g travelling horizontally with a velocity of 150ms−1 strikes a stationary wooden block and come to rest in 0.03s. Calculate the distance of penetration of the bullet into the block. Also, Calculate the magnitude of the force exerted by the wooden block on the bullet,
View SolutionA bullet of mass 40 g moving with a speed of 90ms−1 enters a heavy wooden block and is stopped after a distance of 60 cm . The average resistive force exerted by the block on the bullet is :
View Solution
