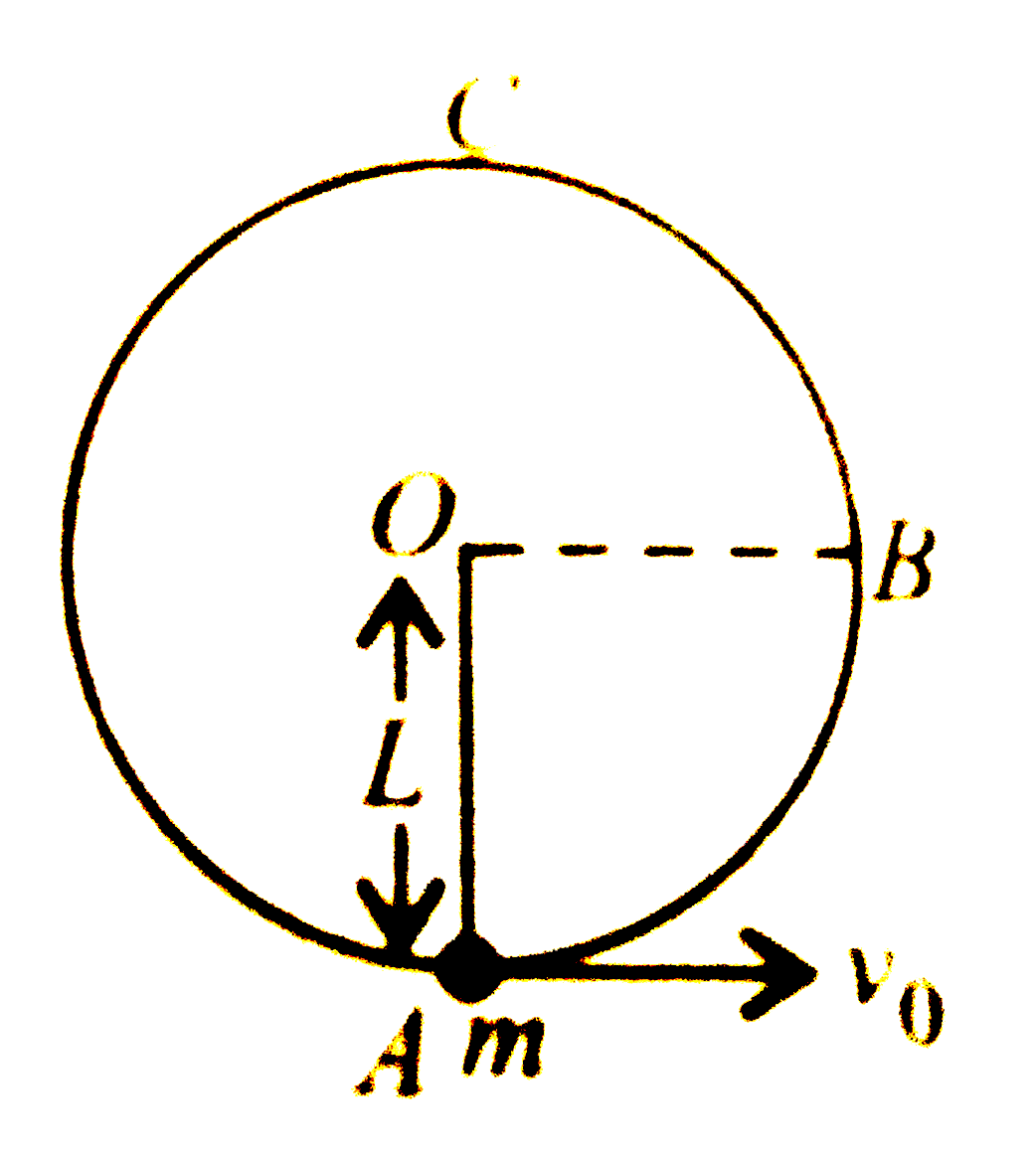
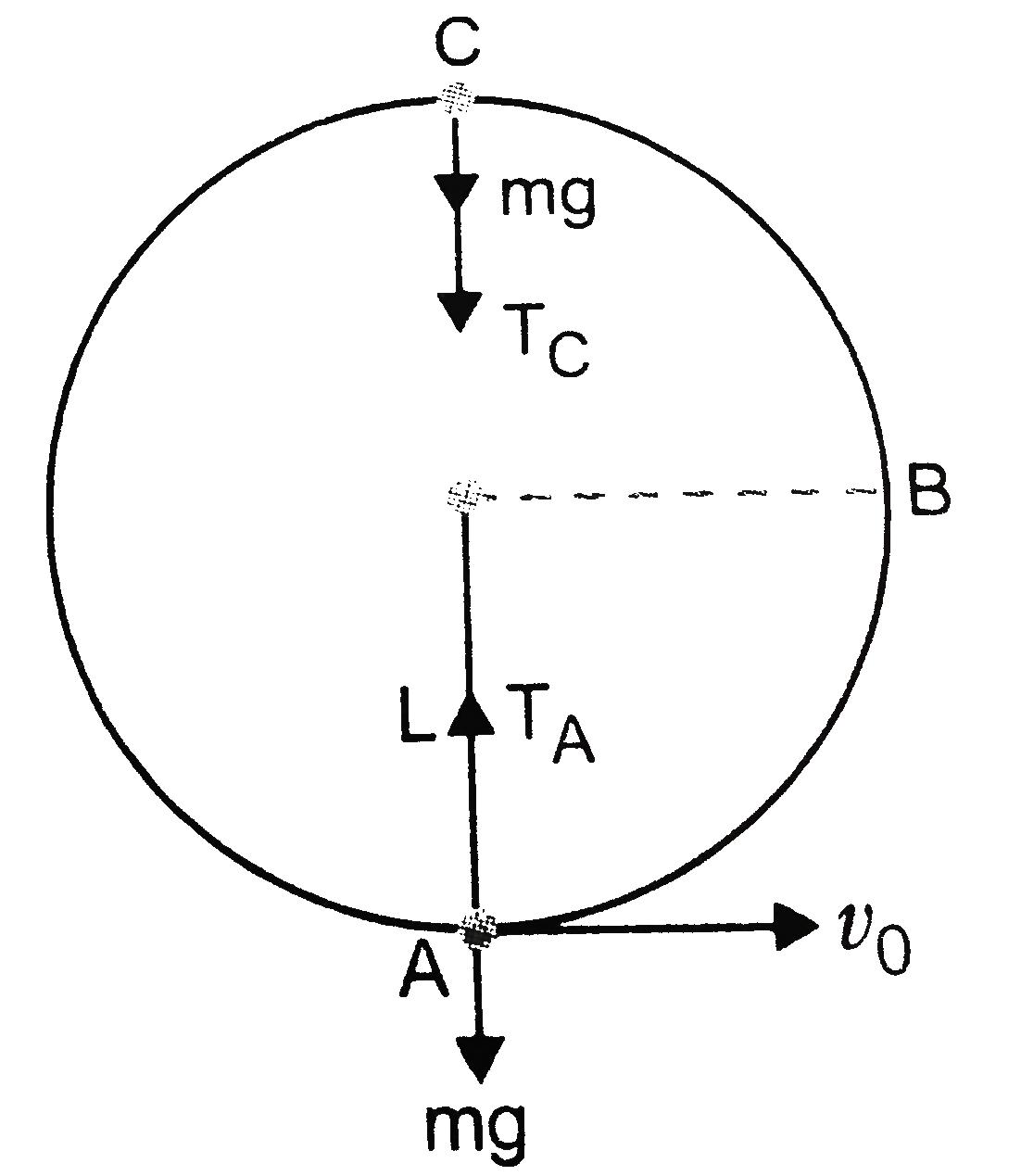
A bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a circle in the vertical plane.
Match the Column I with Column II.

Let horizontal velocity at lowest pint A be VA such that string becomes slack only on reaching highest point C. Taking the potential energy of the system to be zero at A, the total mechanical energy, E
At A:
E=12mv2A ...(i)(E=KE+PE=KEasPE=0)
TA−mg=mv2Ar ...(ii)(Using Newron'sIIndLaw)
Where TA is the tension in the string at Agt
At the highest point C, the string slackent, so Tc=0
At C:
E=12mv2c+2mgr ...(ii)(Wherevcis the velocity at C.)
mg=mv2cr ...(iv)(Nowron'sIIndlaw)
From equation (iv),12mv2c=12mgr
Put this value in equation (iii)
E=12mg+2mgr
E=52mgr ...(v)(This is alos KE at A asPEA=0)
From equations(i) & (v)
12mv2A=52mgr
vA=√5gr ...(vi)
At B:
E=12mv2B+mgr (x) (WherevBis the velocity at B)
This should be same as teh energy at A.
So, 12mv2B+mgr=12mv2A=52mgr(Using equation(viii))
12mv2B=32mgr
⇒vB=√3gr ...(ξ)
kinetic energy at B=32mgr ...(ξi).
At C, the string becomes slack and velocity of bob is horizontal and the left, Bob cntinus on its circular path and completes the revolution.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION
2 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF
95 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A bob is attached to a string of length l whose other end is fixed and is given horizontal velocity at the lowest point of the circle so that the bob moves in a vertical plane. Match the velocity given at the lowest point of circle in column I with tension and velocity at the highest point of the circle corresponding to velocity of column I of column II

View SolutionA bob of mass M is suspended by a massless string of length L. The horizontal velocity v at position A is just sufficient to make it reach the point B. The angle θ at which the speed of the bob is half of that at A, satisfies
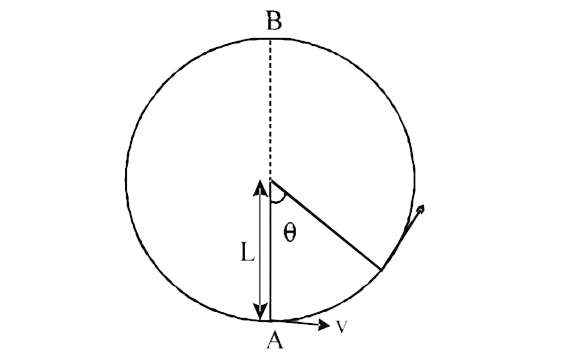
View Solution
Knowledge Check
A bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) v0 (ii) the speeds at points B and C, (ii) the ration of kinetic energies (KB/KC) at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
 AA-p,B-q,C-s,D-rBA-q,B-r,C-q,D-sCA-r,B-s,C-q,D-pDA-s,B-p,C-r,D-q
AA-p,B-q,C-s,D-rBA-q,B-r,C-q,D-sCA-r,B-s,C-q,D-pDA-s,B-p,C-r,D-qA bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio l1l2 is
A1B3C5D1/5
A bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio l1l2 is
View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure . What will be the trajectory of the particle if the string is cut at
(a) Point B ? (b) Point C? (c) Point X?
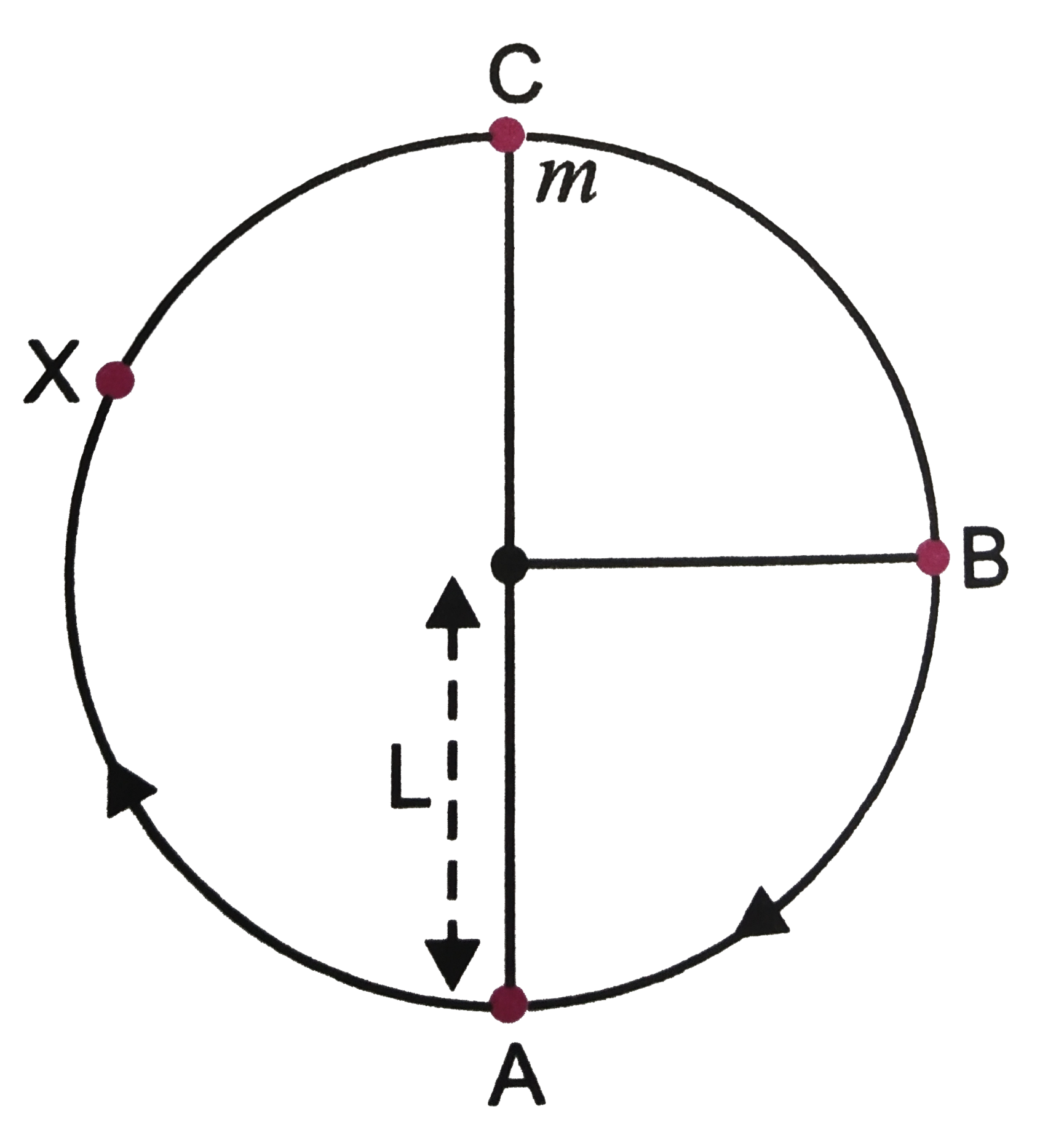
View SolutionA particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is v0 to complete the vertical circle. The tension in the string when it becomes horizontal is
View SolutionThe maximum velocity at the lowest point, so that the string just slack at the highest point in a vertical circle of radius l.
View SolutionA particle of mass m is suspended by a string of length l from a fixed rigid support. A sufficient horizontal velocity =√3gl is imparted to it suddenly. Calculate the angle made by the string with the vertical when the accekleration of the particle is inclined to the string by 45∘ .
View SolutionA positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.

View Solution
