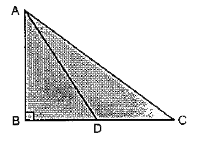
In a right-angled triangle ABC,∠ABC=90∘ and D is mid-point of AC. Prove that BD=12AC.
The correct Answer is:12AC
Step by step video, text & image solution for In a right-angled triangle ABC, angleABC=90^(@) and D is mid-point of AC. Prove that BD=(1)/(2)AC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)Book:ICSEChapter:MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)Exercise:EXERCISE 12(A)
Explore 23 Videos
- MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)Book:ICSEChapter:MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)Exercise:EXERCISE 12(B)
Explore 23 Videos
- MENSURATION (PLANE FIGURE) Book:ICSEChapter:MENSURATION (PLANE FIGURE) Exercise:TOPIC-3 (4 Marks Questions)
Explore 8 Videos
- MID-POINT THEOREMBook:ICSEChapter:MID-POINT THEOREMExercise:4 MARKS QUESTION
Explore 15 Videos
Similar Questions
In the given figure, triangle ABC is a right triangle with ∠B=90∘andD is mid-point of side BC. Prove that :
AC2=AD2+3CD2
View SolutionIn right-angled triangle ABC in which ∠C=90∘ , if D is the mid-point of BC , prove that AB2=4 AD2−3 AC2 .
View SolutionIn a triangle ABC,B=90∘ and D is the mid-oint of BC then prove that AC2=AD2+3CD2
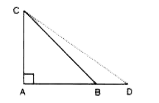
View SolutionIn triangle ABC, angle A=90∘,CA=AB and D is a point on AB produced. Prove that:
DC2−BD2=2AB.AD.
View SolutionIn Fig. 3, ABC is a right triangle, right angled at C and D is the mid-point of BC. Prove that AB2=4AD2−3AC2.
View SolutionIn triangle ABC, AB=AC and BD is perpendicular to AC. Prove that : BD2−CD2=2CD×AD
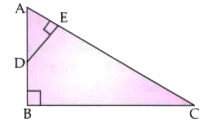
View SolutionABC is a right angled triangle with ∠ABC=90∘, D is any point on AB and DE is perpendicular to AC. Prove that :

(i) ΔADE~ΔACB.
View SolutionIn an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that :
AD2=AC2+BD.CD
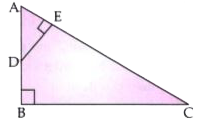
View SolutionABC is a right angled triangle with ∠ABC=90∘, D is any point on AB and DE is perpendicular to AC.
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
View SolutionABC is a right angled triangle with ∠ABC=90∘, D is any point on AB and DE is perpendicular to AC. Prove that :
(iii) Find area of Δ ADE : area of quadrilateral BCED.If AC = 13 cm, BC = 5 cm and AE = 4 cm.
View Solution