In triangle ABC, M is mid-point of AB and a straight line through M and parallel to BC cuts AC at N. Find the lengths of AN and MN, if BC = 7 cm and AC = 5 cm.
The correct Answer is:AN=2.5 cm and MN=3.5 cm
To solve the problem, we will follow these steps:
Step 1: Understand the Geometry of the Triangle
In triangle ABC, M is the midpoint of side AB. A line through M is drawn parallel to side BC, which intersects side AC at point N.
Step 2: Identify the Given Lengths
We are given:
- Length of BC = 7 cm
- Length of AC = 5 cm
Step 3: Use the Midpoint Theorem
According to the Midpoint Theorem, if a line segment is drawn parallel to one side of a triangle and intersects the other two sides, then it divides those sides proportionally. Since M is the midpoint of AB, and the line through M is parallel to BC, point N will also be the midpoint of AC.
Step 4: Calculate Lengths
1. Finding MN: Since MN is parallel to BC and M is the midpoint of AB, MN will be half the length of BC.
MN=12×BC=12×7 cm=3.5 cm
2. Finding AN: Since N is the midpoint of AC, AN will be half the length of AC.
AN=12×AC=12×5 cm=2.5 cm
Final Results
- Length of MN = 3.5 cm
- Length of AN = 2.5 cm
---
In triangle ABC, M is the midpoint of side AB. A line through M is drawn parallel to side BC, which intersects side AC at point N.
We are given:
- Length of BC = 7 cm
- Length of AC = 5 cm
According to the Midpoint Theorem, if a line segment is drawn parallel to one side of a triangle and intersects the other two sides, then it divides those sides proportionally. Since M is the midpoint of AB, and the line through M is parallel to BC, point N will also be the midpoint of AC.
1. Finding MN: Since MN is parallel to BC and M is the midpoint of AB, MN will be half the length of BC.
MN=12×BC=12×7 cm=3.5 cm
AN=12×AC=12×5 cm=2.5 cm
- Length of MN = 3.5 cm
- Length of AN = 2.5 cm
Topper's Solved these Questions
- MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)BOOK - ICSECHAPTER - MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)EXERCISE - EXERCISE 12(B)
23 Videos
- MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)BOOK - ICSECHAPTER - MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)EXERCISE - EXERCISE 12(B)
23 Videos
- MENSURATION (PLANE FIGURE) BOOK - ICSECHAPTER - MENSURATION (PLANE FIGURE) EXERCISE - TOPIC-3 (4 Marks Questions)
8 Videos
- MID-POINT THEOREMBOOK - ICSECHAPTER - MID-POINT THEOREMEXERCISE - 4 MARKS QUESTION
15 Videos
Similar Questions
In triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q and a line through Q and a line through Q and parallel to BC meets median AP at point R. Prove that :
BC=4QR.
View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Find AB, if EF=4.8cm.
View SolutionABC is a triangle right angled at C and M is mid-point of hypotenuse AB. Line drawn through M and parallel to BC intersects AC at D. Show that:
MD is mid-point of AC.
View SolutionIn triangle ABC, P is mid-point of AB and Q is mid-point of AC. If AB = 9.6 cm, BC = 11 cm and AC = 11.2 , find the perimeter of the trapezium PBCQ.
View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Prove that BDFE is a parallelogram
View SolutionIn the given figure, triangle ABC is circumscribing a circle. Find the length of BC, if AF=3 cm, FB=4 cm and AC= 9 cm
View SolutionIn triangle ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm, find the perimeter of the parallelogram BDEF.
View SolutionIn triangle ABC, M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use Intercept Theorem to show that MN bisects AD.
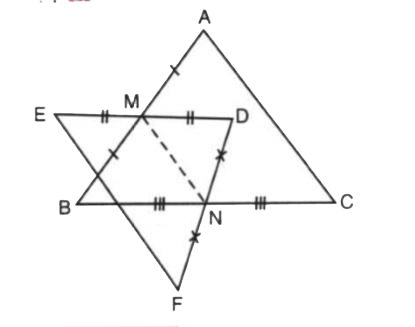
View SolutionIn the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF. Show that : EF = AC.
View SolutionIn triangle ABC, D and E are mid-points of sides AB and BC respectively. Also, F is a point in side AC so that DF is parallel to BC
Find the perimeter of parallelogram DBEF, if AB = 10 cm, BC = 8.4 cm and AC = 12 cm.
View Solution
