Choose the lengths of the sides yourself and draw one equilateral, one isosceles and one scalene triangle.
Isosceles triangle :
In △PQR, l(QR) = 5.8 cm, l(PQ) = l(PR) = 4.7 cm
 Solution in Marathi
Solution in Marathi
The figure of triangle △PQR, l(QR) = 5.8 cm, l(PQ) = l(PR) = 4.7 cm is as given below 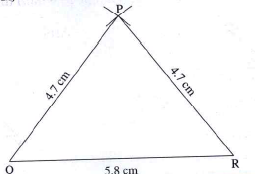
Topper's Solved these Questions
Similar Questions
If 7 kg of onions cost ₹ 140, how much must we pay for 12 kg of onions ?
View SolutionWhich number is neither a prime number nor a composite number?
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionConstruct a parallelogram PQRS, when PQ=3.7cm,QR=2.3cm,andPR=4.8cm.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_VII_C05_S01_021_Q01.png" width="80%"gt
View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionConstruct an isosceles triangle PQR where PQ = PR and ∠Q=50∘, QR = 7 cm. Also draw its circumcircle.
View SolutionIn Δ PQR, l(PQ) = 4 cm, l (QR) = 4 cm, l (PR) = 8 cm. Can you draw this triangle ? Why ?
View SolutionAnswer the following question :
In Δ PQR, l(PQ) = 4 cm, l (QR) = 4 cm, l (PR) = 8 cm. Can you draw this triangle ? Why ?
View SolutionDraw the triangle with the measures given below:
In △PQR, l(PQ) = 6 cm, l(QR) = 3.8 cm, l(PR) = 4.5 cm.
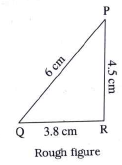
View SolutionDraw an isosceles triangle with base 5 cm and the other sides 3.5 cm each.
Let △XYZ be an isosceles triangle in which the base YZ = 5 cm and l(XY) = l(XZ) = 3.5 cm.

View SolutionChoose the lengths of the sides yourself and draw one equilateral, one isosceles and one scalene triangle.
Equilateral triangle :
In △ABC, l(AB) = l(BC) = l(AC) = 4.2 cm
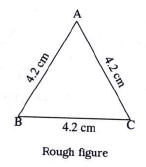
View SolutionChoose the lengths of the sides yourself and draw one equilateral, one isosceles and one scalene triangle.
Scalene triangle :
In △DEF, l(DE) = 4 cm, l(EF) = l(PR) = 5 cm, l(DF) = 6 cm
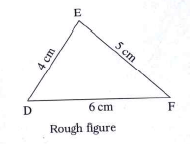
View Solution
