In PQR, l(PQ) = 4 cm, l (QR) = 4 cm, l (PR) = 8 cm. Can you draw this triangle ? Why ?
Step by step video & image solution for In Delta PQR, l(PQ) = 4 cm, l (QR) = 4 cm, l (PR) = 8 cm. Can you draw this triangle ? Why ? by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Related Playlists
Similar Questions
In ΔPQR,PQ=4 cm, PR = 6 cm and QR = 3 cm . Which of the following is correct ?
View SolutionIn ΔPQR,PQ=4cm,PR=6cmandQR=3cm. Which of the following is correct?
View SolutionIn ΔPQR,PQ=6√3cm,PR=12cmandQR=6cm then ∠Q is
View SolutionIn ΔPQR,PQ=4cm,PR=6cmandQR=3cm. Which of the following is correct?
View SolutionIn Δ PQR, PQ = 4 cm, QR = 3 cm, and RP = 3.5 cm. Δ DEF is similar to Δ PQR. If EF = 9 cm, then what is the perimeter of Δ DEF ?
View SolutionDraw a ΔABC with AB = 4 cm, BC = 6 cm and CA = 3 cm. Draw another ΔPQR with PQ = 4 cm, QR = 6 cm and RP = 3 cm. State about the congruency of triangles.
 View Solution
View SolutionIn △PQR,PQ=10 cm , QR =12 , PR =8 cm . Find out the greatest and the smallest angle of the triangle .
View SolutionIn the given figure L, M and N are mid point of the sides PQ, PR and QR respectively of ΔPQR. If PQ = 4.4 cm, QR = 5.6 cm and PR = 4.8 cm then find the perimeter of ΔLMN.
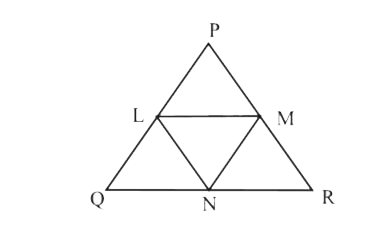 View Solution
View Solution△ABC~△PRQ and PQ = 4 cm, QR = 7 cm and PR = 8 cm. If ar(△ABC):ar(△PRQ) = 1 : 4 , then AC is equal to :
△ABC~△PRQ है और PQ =4 cm, QR = 7 cm तथा PR = 8 cm है । यदि ar(△ABC):ar(△PRQ) = 1 : 4 है, तो AC का मान क्या होगा ?View Solution△PQR~△LTR. In △PQR,PQ=4.2 cm, QR=5.4 cm, PR=4.8 cm. Construct △PQR and △LTR, such that PQLT=34.
View Solution


