What is the wavelength of a beam of X -rays (in Ao ) which is difted by a crystal in a direction making an angle of 60∘ with the incident beam and corresponding to first order reflection from crystal lattice planes separated by 3×10−10m?
The correct Answer is:3
To find the wavelength of the X-rays diffracted by a crystal, we can use Bragg's Law, which is given by the equation:
2Dsinθ=nλ
Where:
- D is the distance between the crystal lattice planes,
- θ is the angle of diffraction,
- n is the order of reflection (in this case, n=1),
- λ is the wavelength of the X-rays.
1. Identify the Given Values:
- The distance between the lattice planes, D=3×10−10 m.
- The angle of diffraction, θ=60∘.
- The order of reflection, n=1.
2. Substitute the Values into Bragg's Law:
2Dsinθ=nλ
Substituting the known values:
2×(3×10−10)×sin(60∘)=1×λ
3. Calculate sin(60∘):
sin(60∘)=√32
4. Substitute sin(60∘) into the Equation:
2×(3×10−10)×√32=λ
5. Simplify the Equation:
3×10−10×√3=λ
6. Calculate the Value of λ:
- We know √3≈1.732, so:
λ=3×10−10×1.732
λ≈5.196×10−10 m
7. Convert the Wavelength to Angstroms:
- Since 1 Ao=10−10 m:
λ≈5.196×10−10 m=5.196×101 Ao≈51.96 Ao
Final Answer:
The wavelength of the X-rays is approximately 51.96 Ao.
---
- D is the distance between the crystal lattice planes,
- θ is the angle of diffraction,
- n is the order of reflection (in this case, n=1),
- λ is the wavelength of the X-rays.
- The distance between the lattice planes, D=3×10−10 m.
- The angle of diffraction, θ=60∘.
- The order of reflection, n=1.
2Dsinθ=nλ
Substituting the known values:
2×(3×10−10)×sin(60∘)=1×λ
sin(60∘)=√32
2×(3×10−10)×√32=λ
3×10−10×√3=λ
- We know √3≈1.732, so:
λ=3×10−10×1.732
λ≈5.196×10−10 m
- Since 1 Ao=10−10 m:
λ≈5.196×10−10 m=5.196×101 Ao≈51.96 Ao
The wavelength of the X-rays is approximately 51.96 Ao.
Topper's Solved these Questions
Similar Questions
What will be the wavelength of the X-rays which give a diffraction angle 2θ equal to 16.80∘ for a crystal ? The interplanar distance in the crystal is 0.200 nm and only the diffraction of the first order is absorbed.
View SolutionThe first order reflection of a beam of X-rays of wavelength 1.54 Ã… from the (100) face of a crystal of the simple cubic type occurs at an angle of 11.29∘ . Calculate the length of the unit cell.
View Solution
Knowledge Check
A beam of protons enters a uniform magnetic field of 0.3T with velocity of 4×105m/s in a direction making an angle of 60∘ with the direction of magnetic field. The path of motion of the particle will be
AcircularBStraight lineCSpiralDhelicalIn Davisson-Germer experiment, an electron beam of 60eV energy falls normally to the surface of the crystal and maximum intensity is obtained at an angle of 60∘ to the direction of incident beam. The inter- atomic distance in the lattice plane of the crystal is
A18ÅB3.6ÅC1.8 ÅD0.18ÅThe second order Grag diffraction of X-rays with λ=1.0 Å from a set of parallel planes in a metal occurs at an angle of 60∘. The distance between the scattering planes in the crystal is
A0.575 ÅB1.00 ÅC2.00 ÅD1.15 Å
A parallel beam of light falls normally on the first face of a prism of small angle .At the second face it is partly reflected,the reflected beam striking at the first face again, and emerging from it in a direction making an angle 6∘ 30' with the reversed direction of the incident beam. The refracted beam is found to have undergone a deviation of 1∘15' from the original direction.Find the refractive index of the glass and the angle of the prism.
View SolutionA beam of X-rays with wavelength λ falls at a glancing angle 60.0∘ on a linear chain of scattering centres with period a. Find the angles of incidence corresponding to all diffraction maxima if λ=2a/5.
View SolutionWhat should be the wavelength (in Å ) of X-ray used for getting the first order Bragg reflection at a glancing angle of 14.7∘ for a crystal having a distance of 4 Å between its two parallel planes? (Considercos 75.3∘ = 0.25)
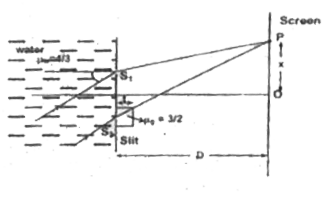
View SolutionA coherent beam light of intensity I and absolute wavelength λ=5000Å is being incident on the slits making an angle 30∘ with horizontal. If screen is placed at a distance D=1 m from the slits and the separation between- the slits is 3×10−4m. A thin film of glass μg= 3/2 and thickness 0.41 mm is placed near one slit as shown in the figure, find
(a) the position of central maxima.
(b) the intensity at'point O.
View SolutionCalculate the wavelength of X rays which produces a diffraction angle 2θ equal to 16.80∘ for a crystal assume first order diffraction with inter particle distance in crystal of 0.2nm
View Solution
