A point mass is subjected to two simultaneous sinusoidal displacement in x -direction, x1(t)=Asinωt and x2(t)=Asin(ωt+π2). Adding a third sinusoidal displacement x3t=Bsin(ωt+ϕ) brings the mass to a complete rest. The value of ϕ is nπ4. Then n is.
The correct Answer is:5
To solve the problem, we need to analyze the given sinusoidal displacements and find the value of n such that the third displacement x3 brings the mass to a complete rest.
Step 1: Understand the given displacements
We have two displacements:
1. x1(t)=Asin(ωt)
2. x2(t)=Asin(ωt+π2)
The second displacement can be rewritten using the sine function:
x2(t)=Acos(ωt)
This is because sin(θ+π2)=cos(θ).
Step 2: Resultant of the first two displacements
The resultant displacement xr(t) of the two displacements can be found using vector addition:
xr(t)=x1(t)+x2(t)=Asin(ωt)+Acos(ωt)
Step 3: Express the resultant in a single sinusoidal form
To combine Asin(ωt) and Acos(ωt), we can use the following formula:
R=√A2+A2=√2A2=A√2
The angle θ can be found using:
tan(θ)=AA=1
Thus, θ=π4.
Therefore, we can express the resultant as:
xr(t)=A√2sin(ωt+π4)
Step 4: Introduce the third displacement
We introduce the third displacement:
x3(t)=Bsin(ωt+ϕ)
We want the total displacement to be zero for the mass to come to rest:
xr(t)+x3(t)=0
Step 5: Condition for complete rest
For the mass to come to rest, the amplitude of the third displacement must equal the amplitude of the resultant displacement but in the opposite direction:
Bsin(ωt+ϕ)=−A√2sin(ωt+π4)
Step 6: Determine the phase difference
To achieve this, we need:
ϕ=π4+π=5π4
Step 7: Find the value of n
We are given that ϕ=nπ4. Setting this equal to our found value:
nπ4=5π4
Dividing both sides by π4:
n=5
Final Answer
Thus, the value of n is:
5
We have two displacements:
1. x1(t)=Asin(ωt)
2. x2(t)=Asin(ωt+π2)
x2(t)=Acos(ωt)
This is because sin(θ+π2)=cos(θ).
The resultant displacement xr(t) of the two displacements can be found using vector addition:
xr(t)=x1(t)+x2(t)=Asin(ωt)+Acos(ωt)
To combine Asin(ωt) and Acos(ωt), we can use the following formula:
R=√A2+A2=√2A2=A√2
The angle θ can be found using:
tan(θ)=AA=1
Thus, θ=π4.
xr(t)=A√2sin(ωt+π4)
We introduce the third displacement:
x3(t)=Bsin(ωt+ϕ)
We want the total displacement to be zero for the mass to come to rest:
xr(t)+x3(t)=0
For the mass to come to rest, the amplitude of the third displacement must equal the amplitude of the resultant displacement but in the opposite direction:
Bsin(ωt+ϕ)=−A√2sin(ωt+π4)
To achieve this, we need:
ϕ=π4+π=5π4
We are given that ϕ=nπ4. Setting this equal to our found value:
nπ4=5π4
n=5
Thus, the value of n is:
5
Topper's Solved these Questions
Similar Questions
Knowledge Check
A point mass is subjected to two simultaneous sinusoidal displacement in x−direction, x1(t)=Asinωt and x2(t)=Asin(ω+2π3). Adding a third sinusoidal displacement x3(t)=Bsin(ωt+ϕ) brings the mass to complete rest. The value of B and ϕ are
A√2A,3π4BA,4π3C√3A,5π6DA,π3A point mass is subjected to two simultaneous sinusoidal displacement in x-direction, x1(t)=Asinωt and x2(t)=Asin(ωt+2π/3). Adding a third sinusoidal displacement x3(t)=Bsin(ωt+ϕ) brings the mass to a complete rest. The values of B and ϕ are :
A√2A,3π4BA,4π3C√3A,5π6DA,π3A point mass is subjected to two simultaneous sinusoidal displacements in x−direction,x1(t)=Asin(ω)tandx2(t)=Asin((ωt+2π3). Adding a third sinusoidal displacement x3(t)=Bsin(ωt+ϕ) brings the mas to a complete rest. The values of (B) and (phi) are.
A√2A,3π4BA,4π3C√3A,5π3DA,π3
A partical is subjucted to two simple harmonic motions
x1=A1sinωt
and x2=A2sin(ωt+π/3)
Find(a) the displacement att=0, (b) the maximum speed of the partical and ( c) the maximum acceleration of the partical.
View SolutionThe displacements of two interfering light waves are y1=2sinωt and y2=5sin(ωt+π3) the resultant amptitude is
View SolutionTwo sinusoidal current are given by
i1=20sin(ωt+π6)andi2=10sin(ωt−π4)
The pahase difference between them is
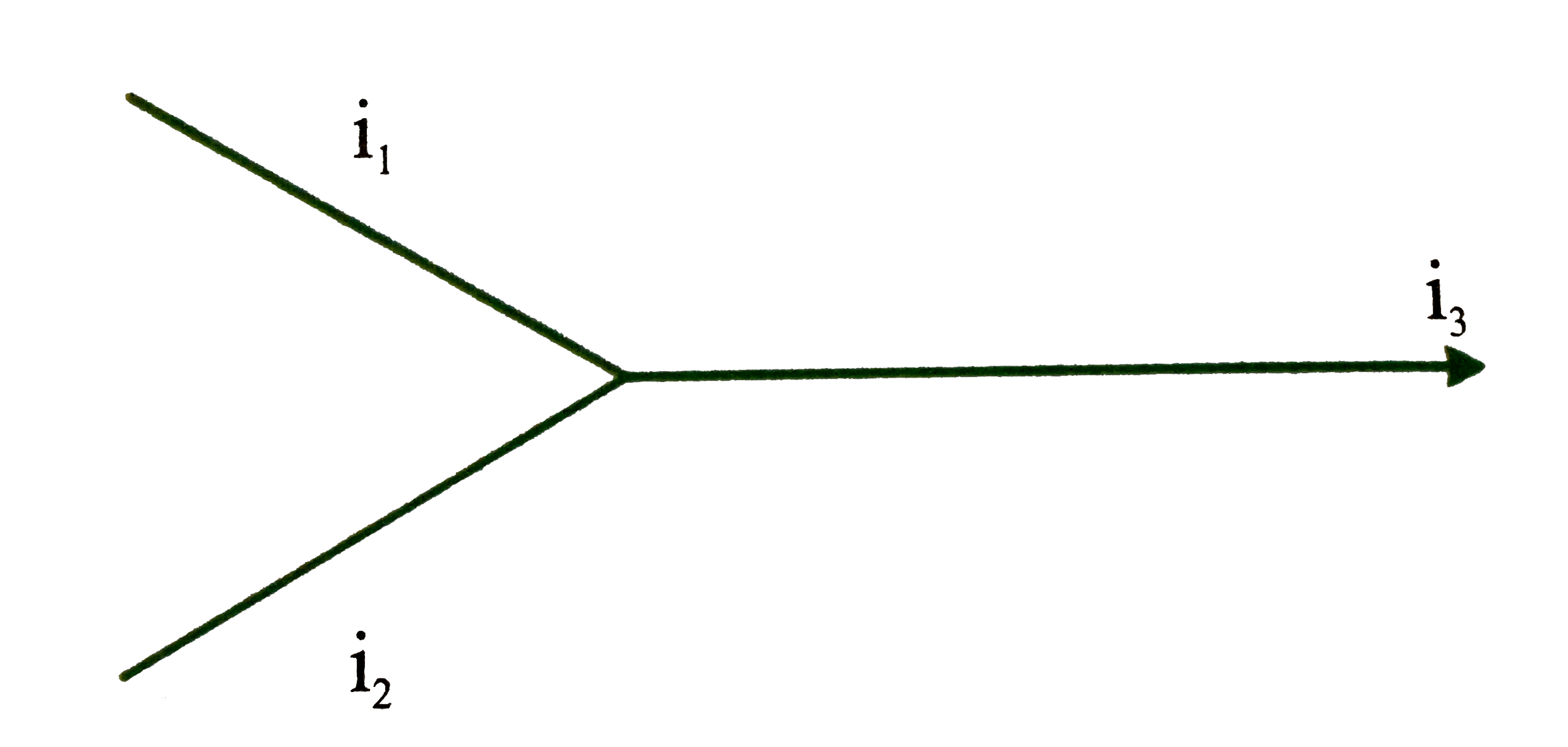
View SolutionIf i1=i0sin(ωt),i2=i02sin(ωt+ϕ), then i3=
View SolutionThe ratio of amplitudes of following SHM is x1=Asinωtandx2=Asinωt+Acosωt
View Solution