Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then 2r equals:Solution in Kannada
√PQt×RS
PQ+RS2
2PQ×RSPQ+RS
√PQ2×RS22
The correct Answer is:A
Step by step video, text & image solution for Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then 2r equals: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The term containing x3 in the expansion
(√x5+3√x3)6 appears in
View SolutionWhich one of the following is not correct for the features of exponential function given by f(x)=bx where b>1 ?
View SolutionLet PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. PS and RQ intersect at a point X on the circumference of the circle. If PQ = 9 and RS = 4, then the diameter of the circle is :
View SolutionIn the given figure, a diameter PQ of a circle bisects the chord RS at the point O. If PS is parallel to RQ, prove that RS is also a diameter of the circle.
View SolutionLet PQ and RS be tangent at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQ×RS .
View SolutionLet PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle,then 2r equals
View SolutionPR is a diameter of a circle. A tangent is draewn at the point P and a point S is taken on the tangent of the circle is such a way that PR=PS. If RS intersects the circle at the point T., prove that ST =PT.
View SolutionIn the adjoining figure, point Q is the point of contact of tangent and circle . If PQ = 12, PR = 8, then find Ps and RS .
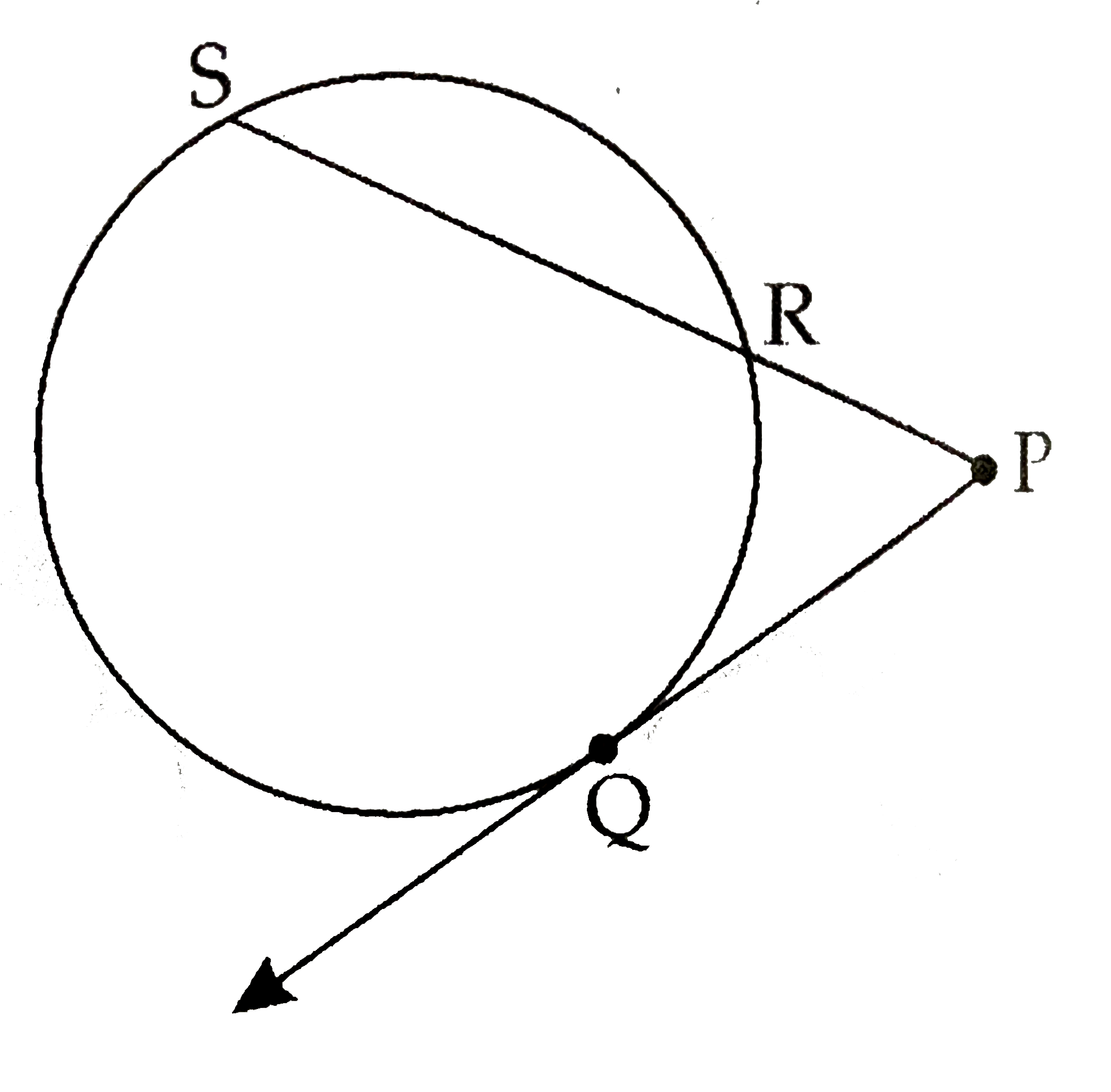
View SolutionLet PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then 2r equals:
View SolutionDraw a circle whose PR is a diameter. Draw a tangent to the point P and take the point S above the tangent so that PR = PS. When RS intersects the circle at the point T, prove that ST = RT = PT.
View SolutionLet PQ and RS be tangent at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQ×RS .
View SolutionIn the given figure, a diameter PQ of a circle bisects the chord RS at the point O. If PS is parallel to RQ, prove that RS is also a diameter of the circle.
View Solutionमाना त्रिज्या r के वृत्त के व्यास PR के सिरों पर स्पर्श रेखायें PO तथा RS हैं। यदि PS तथा RQ, वृत्त की परिधि के बिन्दु X पर प्रतिच्छेदित हो, तो 2r बराबर है
View SolutionIn the adjoining figure, point Q is the point of contact of tangent and the circle. If PQ=12, PR=8, then find PS and RS.
View SolutionLet PQ and RS be tangents at the extremities of one diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, than 2r√PQ⋅RS equals_____
View Solutionमाना PQ और RS त्रिज्या r के एक वृत्त के व्यास PR के सिरों पर स्पर्श रेखाएँ हैं । यदि PS और RQ वृत्त की परिधि पर एक बिंदु X पर प्रतिच्छेद करते हैं, तब 2r का मान बराबर है
View Solution
