The rate of change of concentration of (A) for reaction:
A→B is given by −d[A]dt=k[A]13
The half-life period of the reaction will be:Solution in Bengali
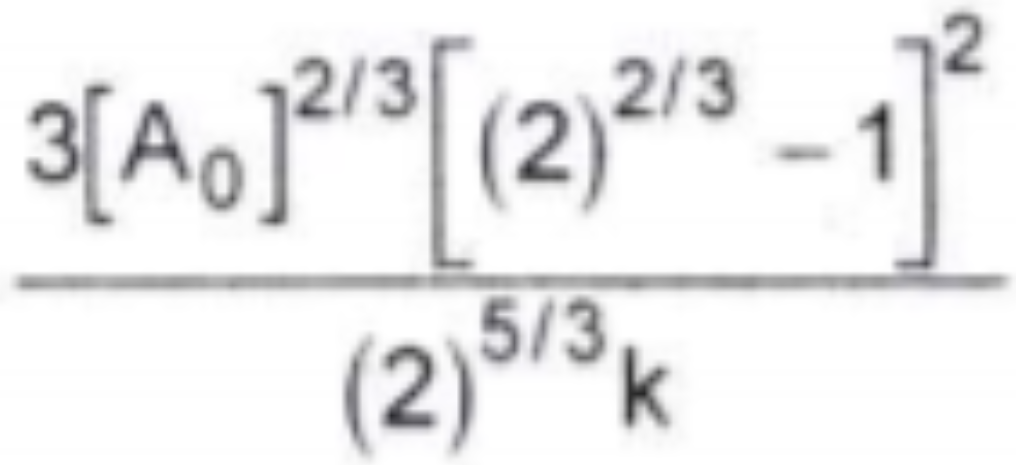
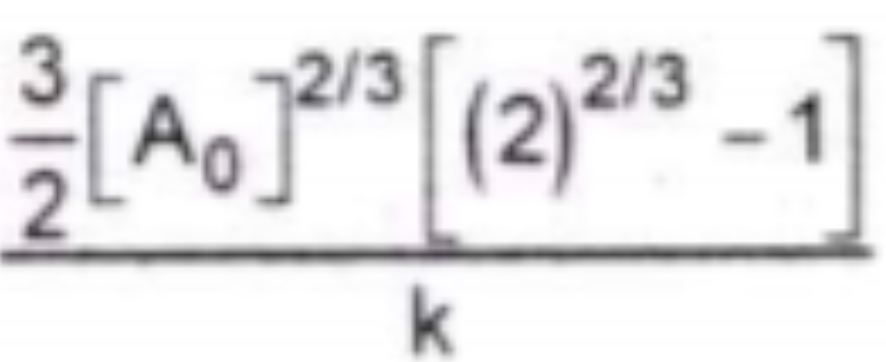
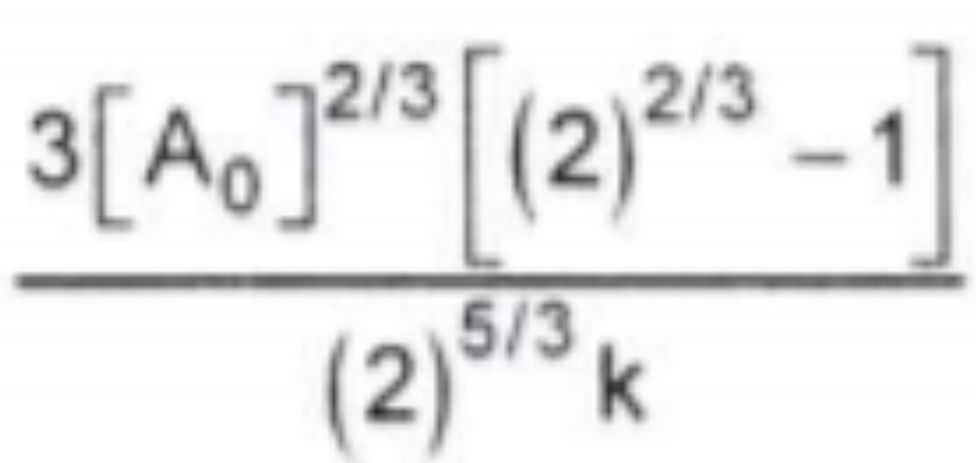
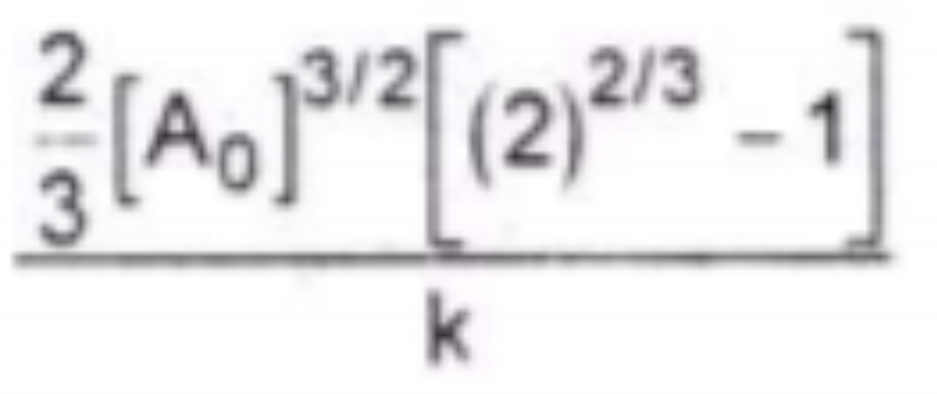
The correct Answer is:C
Step by step video, text & image solution for The rate of change of concentration of (A) for reaction: ArarrB is given by (-d[A])/dt=k[A]^1/3 The half-life period of the reaction will be: by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Which has higher conductance and why? Silver wire at 30∘C or silver wire at 50∘C?
View SolutionFor the reaction: aA + bB rarr cC+dD Rate = (dx)/(dt) = (-1)/(a)(d[A])/(dt) = (-1)/(b)(d[B])/(dt) = (1)/( c)(d[C])/(dt) = (1)/(d)(d[D])/(dt) A reaction follows the given concentration-time graph. The rate for this reaction at 20 s will be
View SolutionIn a first-order reaction A→B, if K is the rate constant and initial concentration of the reactant is 0.5M, then half-life is
View SolutionFor a first order reaction with rate constant 'k' and initial concentration 'a', the half-life period is given by
View SolutionFor a reaction A+3B→P, Rate = −d[A]dt ,the expression for the rate of reaction in terms of change in the concentration of B,−d[B]dt will be :
View SolutionThe rate equation for a reaction A to B is r = k [A]^(0) . If the initial concentration of the reaction is a mol dm^(-3) , the half-life period of the reaction is
View SolutionThe rate law equation for the reaction A to B is found to be -(d[A])/(dt)=k[A]^(1//2) If [A]_(0) were the initial concentration of A, derive expressions for (i) rate constant in the integrated form (ii) half-life period of the reaction
View SolutionThe rate of change of concentration of (A) for reaction A to B is given by -(d[A])/(dt)=k[A]^(1//3) Derive expression for half-life period of the reaction.
View SolutionFor a reaction A + B → product, the rate of the reaction was doubled when the concentration of A alone was reduced to half. Half life of reaction is doubled when concentration of B is reduced to half keeping concentration of A constant. Then order of reaction with respect to A and B are :
View SolutionConsider the reaction : A rarr B + C . Initial concentration of A is 1 M. 20 minutes time is required for completion of 20% reaction. If (d[B])/(dt) =k[A], then calculate half life (t_(1//2)) of reaction.
View SolutionThe rate equation for a reaction A→B is r=k[A]0. If the initial concentration of the reactant is a mol dm−3, the half life period of the reaction is
View SolutionFor a first order reaction with rate constant 'k' and initial concentration 'a', the half-life period is given by
View SolutionIn a first-order reaction A rarr B , if K is the rate constant and initial concentration of the reactant is 0.5 M , then half-life is
View SolutionFor a first order reaction with rate constant k and initial concentration a, the half-life period is given by
View SolutionIn a first-order reaction A→B, if K is the rate constant and initial concentration of the reactant is 0.5M, then half-life is
View Solution
