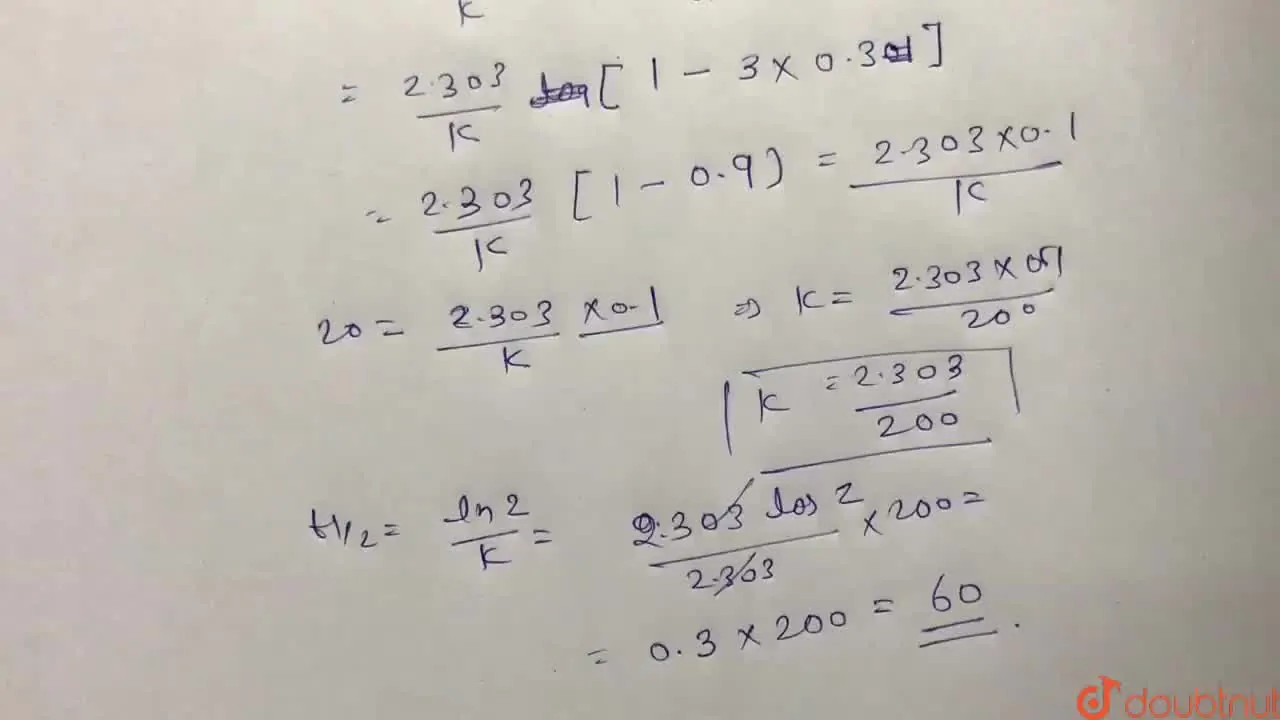Consider the reaction : A→B+C. Initial concentration of A is 1 M. 20 minutes time is required for completion of 20% reaction. If d[B]dt=k[A], then calculate half life (t1/2) of reaction.
62.13 min
Related Playlists
- BOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise - 4 (Level - I)18videos
Chemical Kinetics
- BOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise - 4 (Level - II)15videos
Chemical Kinetics
- BOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise - 2 (Level-II) (COMPREHENSION - 5)1videos
Chemical Kinetics
- BOOK - MOTIONCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise - 420videos
CHEMICAL EQUILIBRIUM
- BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS EXERCISE - Electrochemistry22videos
CLASSROOM PROBLEMS
Similar Questions
Half life time for first order reaction is 25 minutes . What time will be required for 99% completion of reaction ?
View Solution20% first order reaction is completed in "50" minutes.Time required for the completion of 60% of the reaction is
View SolutionShow that in the first order reaction, time required for completion of 99.9% is 10 times that of half-life (t1/2) of the reaction.
View SolutionFor the zero order reaction A→B+C, initial concentration of A is 0.1A. If A=0.08M after 10 minutes, then it's half− life and completion time are respectively :
View SolutionHalf life of a first order reaction is 69.3 minutes. Time required to complete 99.9% of the reaction will be :
View SolutionA first order reaction completes 60% 20 minutes. The time required for the completion of 90% of the reaction is approx………..
View SolutionIf rate constatnt of a chemical reaction is 10−2s−1 then the time required for the completion of 20% of the reaction will e
View SolutionFor the zero order reaction, A→B+C, initial concentration of A is 0.1 M If [A] = 0.08 M after 10 minutes, then it's half life and completion time are respectively
View SolutionA first order reaction is half completed in 45 minutes.The time required to complete 99.9% of the reaction
View SolutionA first order reaction is 20% complete in 10 minutes. Calculate the time for the completion of 75% of the reaction.
View Solution