A particle moves with deceleration along the circle of radius R so that at any moment of time its tangential and normal accelerations are equal in moduli . At the initial moment t=0 the speed of the particle equals v0, then the speed of the particle as a function of the distance covered s will beSolution in Bengali
v=v0e(−sR)
v=v0e(sR)
v=v0e(−Rs)
v=v0e(Rs)
The correct Answer is:A
Step by step video, text & image solution for A particle moves with deceleration along the circle of radius R so that at any moment of time its tangential and normal accelerations are equal in moduli . At the initial moment t=0 the speed of the particle equals v_0, then the speed of the particle as a function of the distance covered s will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The temperature of human body is 98∘F what will be its equivalent in Centigrade scale ?
View SolutionThe Young's modulus of iron and steel are 5×1010N/m2 and 2×1011N/m2 respectively. An iron wire and steel wire of same length are extended by 2 mm under the same force. If the radii of iron and steel wires are RI and RS respectively, then what will be the relation between RI and RS?
View SolutionA point moves with decleration along the circle of radius R so that at any moment of time its tangential and normal accelerations are equal in moduli. At the initial moment t=0 the velocity of the point equals v_0 . Find: (a) the velocity of the point as a function of time and as a function of the distance covered s_1 , (b) the total acceleration of the point as a function of velocity and the distance covered.
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View Solutiona particle is moving in a circle of radius R in such a way that at any instant the normal and the tangential component of its acceleration are equal. If its speed at t=0 is v0 then time it takes to complete the first revolution is Rαv0(1−e−βπ). Find the value of (α+β).
View SolutionA particle moves with deceleration along a circle of radius R so that at any moment its tangential and normal accelerations are equal in moduli. At the initial moment t=0 the velocity of the point equals v_(0) . Find (a) the velocity of the point as a function of t and s , (b) the resultant acceleration modulus as a function of v .
View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
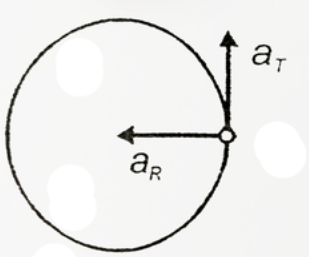
The time after which the speed of particle reduces to half of its initial value is
View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
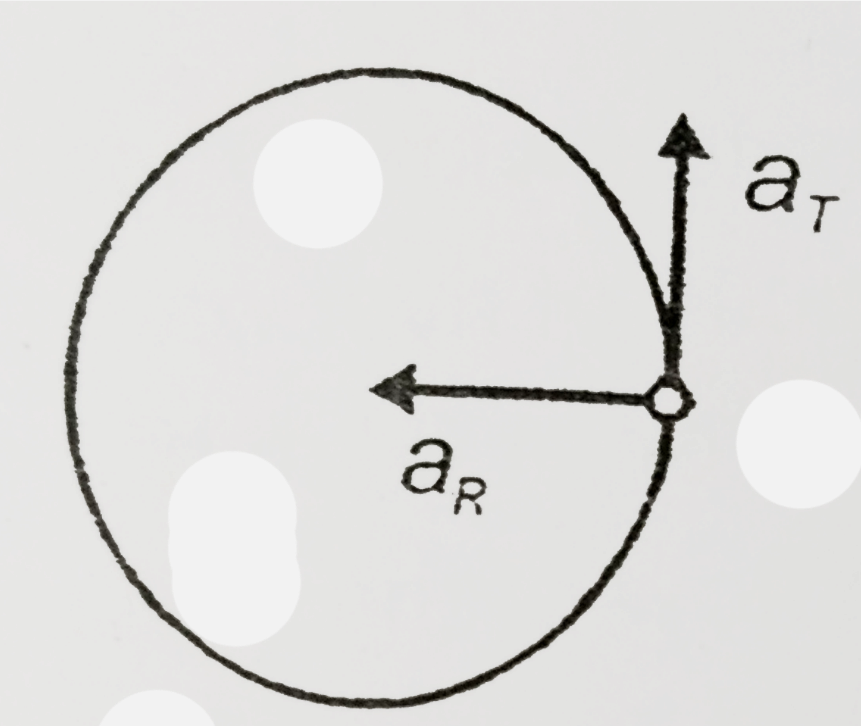
The magnitude of tangential acceleration at t=R2u is
View SolutionA particle is moving in a circle of radius R in such a way that at any instant the tangential retardation of the particle and the normal acceleration of the particle are equal. If its speed at t=0 is v0, the time taken to complete the first revolution is
View SolutionA point moves with decleration along the circle of radius R so that at any moment of time its tangential and normal accelerations
are equal in moduli. At the initial moment t=0 the velocity of the point equals v0. Find:
(a) the velocity of the point as a function of time and as a function of the distance covered s1,
(b) the total acceleration of the point as a function of velocity and the distance covered.
View SolutionA particle is moving in a circle of radius R in such a way that at any instant the normal and tangential components of the acceleration are equal. If its speed at t=0 is u_(0) the time taken to complete the first revolution is :
View SolutionA particle moves with deceleration along the circle of radius R so that at any moment of time its tangential and normal acceleration are equal in moduli. At the initial moment t=0 the speed of the particle equals V0 then
The total acceleration of the particle as function of velocity and distance covered
View SolutionA particle is moving in a circle of radius R in such a way that at any instant the normal and tangential components of its acceleration are equal. If its speed at t=0 is Vo, the time taken to complete the first revolution is
View SolutionA particle is moving on a circle of radius A .At an instant its speed and tangential acceleration are B and C respectively.Total acceleration of the particle at that instant is
View SolutionA particle is moving in a circle of radius R in such a way that at any instant the normal and tangential component of the acceleration are equal. If its speed at t=0 is u0 the time taken to complete the first revolution is
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View Solution
