A particle moves with deceleration along the circle of radius R so that at any moment of time its tangential and normal acceleration are equal in moduli. At the initial moment t=0 the speed of the particle equals V0 then
The total acceleration of the particle as function of velocity and distance coveredSolution in Telugu
a=√2v2R
a=√2vR
a=√2Rv
a=2Rv
The correct Answer is:A
Step by step video, text & image solution for A particle moves with deceleration along the circle of radius R so that at any moment of time its tangential and normal acceleration are equal in moduli. At the initial moment t=0 the speed of the particle equals V_(0) then The total acceleration of the particle as function of velocity and distance covered by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HORIZONTAL CIRCULAR MOTIONBOOK - AAKASH SERIESCHAPTER - HORIZONTAL CIRCULAR MOTIONEXERCISE - PRACTICE SHEET (EXERCISE-III (Applications of Circular Motion (LEVEL-I (Straight Objective Type Questions))))
13 Videos
- HORIZONTAL CIRCULAR MOTIONBOOK - AAKASH SERIESCHAPTER - HORIZONTAL CIRCULAR MOTIONEXERCISE - PRACTICE SHEET (EXERCISE-III (Applications of Circular Motion (LEVEL-II (Straight Objective Type Questions))))
9 Videos
- HORIZONTAL CIRCULAR MOTIONBOOK - AAKASH SERIESCHAPTER - HORIZONTAL CIRCULAR MOTIONEXERCISE - PRACTICE SHEET (EXERCISE-II (LEVEL-II (Straight Objective Type Questions)))
5 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -3
154 Videos
- KINEMATICSBOOK - AAKASH SERIESCHAPTER - KINEMATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED)) (Integer Type Questions)
12 Videos
Similar Questions
A car is moving along a circular track of radius 10√3m with a constant speed of 36kmph. A plumb bob is suspended from the roof of the car by a light rigid rod of length Im. The angle made by the rod with the track is (g=10ms−2 )
View SolutionA vehicle is moving on a banked road θ is angle of banking and μ is coefcient of friction between tyre of vehicle and road. The vehicle is moving along horizontal circular path of radius (r) velocity of vehicle for which it does not slip is 'v'. Choose the correct alternative
View SolutionTwo point size bodies of same mass are knotted to a horizontal string one at the end, and the other at the mid point of it. The string is rotated in horizontal plane with the other end as centre. If T is tension in the string between centre of circles and first body then the tension in the string between the two bodies is
View SolutionA satellite takes 1/8 years to move round the earth in its permissible orbit of radius R. The period when it revolves round the earth in an orbit of radius '2R' is
View SolutionThree particles start from origin at the same time: one with velocity v1 along positive x - axis, the second along the positive y-axis with a velocity v2 and the third along the line y=x with such a speed that all the three always stay in a straight line, then the velocity of the third particle is √kV1V2(V1+V2).
View SolutionA point moves with decleration along the circle of radius R so that at any moment of time its tangential and normal accelerations are equal in moduli. At the initial moment t=0 the velocity of the point equals v_0 . Find: (a) the velocity of the point as a function of time and as a function of the distance covered s_1 , (b) the total acceleration of the point as a function of velocity and the distance covered.
View SolutionA particle moves with deceleration along the circle of radius R so that at any moment of time its tangential and normal acceleration are equal in moduli. At the initial moment t=0 the speed of the particle equals v0, then th speed of the particle as a function of the distance covered S will be
View SolutionA particle moves with deceleration along a circle of radius R so that at any moment its tangential and normal accelerations are equal in moduli. At the initial moment t=0 the velocity of the point equals v_(0) . Find (a) the velocity of the point as a function of t and s , (b) the resultant acceleration modulus as a function of v .
View SolutionA particle is moving along a circular path ofradius R in such a way that at any instant magnitude of radial acceleration & tangential acceleration are equal. 1f at t = 0 velocity of particle is V0. Find the speed of the particle after time t=(R)/(2V0)
View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
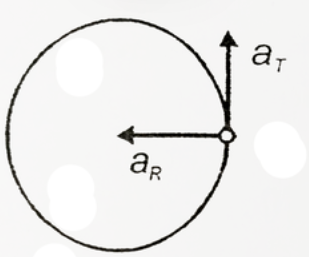
The time after which the speed of particle reduces to half of its initial value is
View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
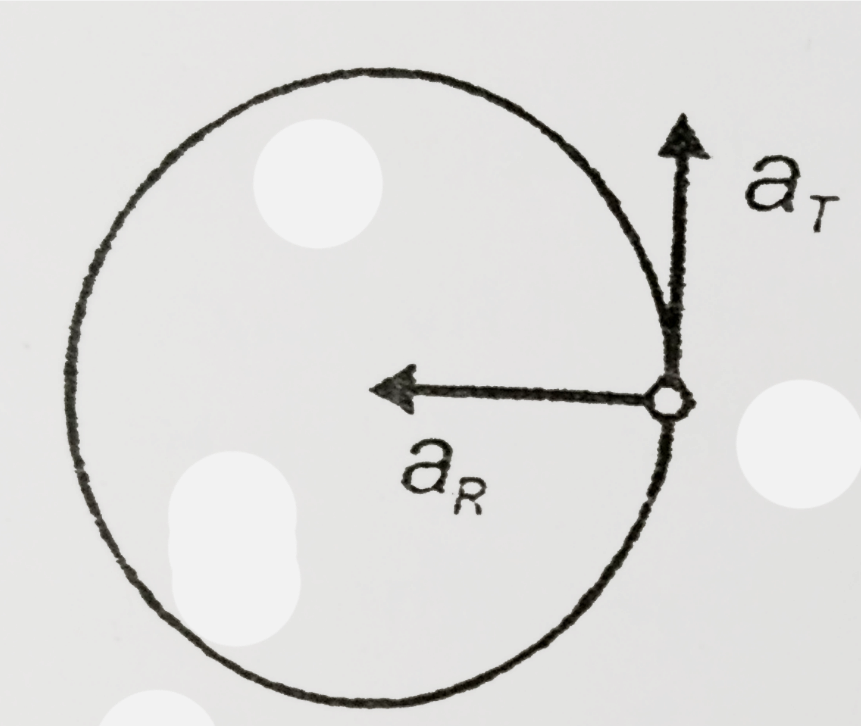
The magnitude of tangential acceleration at t=R2u is
View SolutionA particle is moving in a circle of radius R in such a way that at any instant the tangential retardation of the particle and the normal acceleration of the particle are equal. If its speed at t=0 is v0, the time taken to complete the first revolution is
View SolutionA point moves with decleration along the circle of radius R so that at any moment of time its tangential and normal accelerations
are equal in moduli. At the initial moment t=0 the velocity of the point equals v0. Find:
(a) the velocity of the point as a function of time and as a function of the distance covered s1,
(b) the total acceleration of the point as a function of velocity and the distance covered.
View SolutionA particle moves in a circle in such a way that, its tangential deceleration is numerically equal to its radial acceleration. If the initial velocity of the particle is V0, find the variation of its velocity with time
View SolutionA particle moves with deceleration along the circle of radius R so that at any moment of time its tangential and normal acceleration are equal in moduli. At the initial moment t=0 the speed of the particle equals V0 then
The speed of the particle as a function of the distance coverd will be
View Solution
