A particle is moving along the path given by y=C6t6 (where C is a positive constant). The relation between the acceleration (a) and the velocity (v) of the particle at t = 5 sec isSolution in Bengali
5a = v
a = 5v
a=√v
a = v
The correct Answer is:D
Step by step video, text & image solution for A particle is moving along the path given by y = C/6 t^6 (where C is a positive constant). The relation between the acceleration (a) and the velocity (v) of the particle at t = 5 sec is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find the unit of speed.
View SolutionAn ideal gas has been placed in a tank at 37∘C. The guage pressure is initially 609 kPa. One fourth of the gas is then released from the tank and thormal equilibrium is established. If the temperature is now 317∘C, then the gauge pressure will be
View SolutionA particle moves along the x-direction with constant acceleration. The displacement, measured from a convenient position, is 2 m at time t= 0 and is zero when t= 10 s. If the velocity of the particle is momentary zero when t = 6 s, determine the acceleration a and the velocity v when t= 10s.
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionA particle moves along x-axis with acceleration a=6(t-1) where t is in second. If the particle is initially at the origin and it moves along positive x-axis with v_(0)=2m//s , find the nature of motion of the particle.
View SolutionFor a particle moving along a straight line, its velocity 'v' and displacement 's' are related as v2=cs, here c is a constant. If the displacement of the particle at t=0 is zero, its velocity after 2 sec is:
View SolutionDisplacement (x) of a particle is related to time (t) as x = at + b t^(2) - c t^(3) where a,b and c are constant of the motion. The velocity of the particle when its acceleration is zero is given by:
View SolutionDuring one dimensional motion on x-axis Velocity time graph for particle is given.
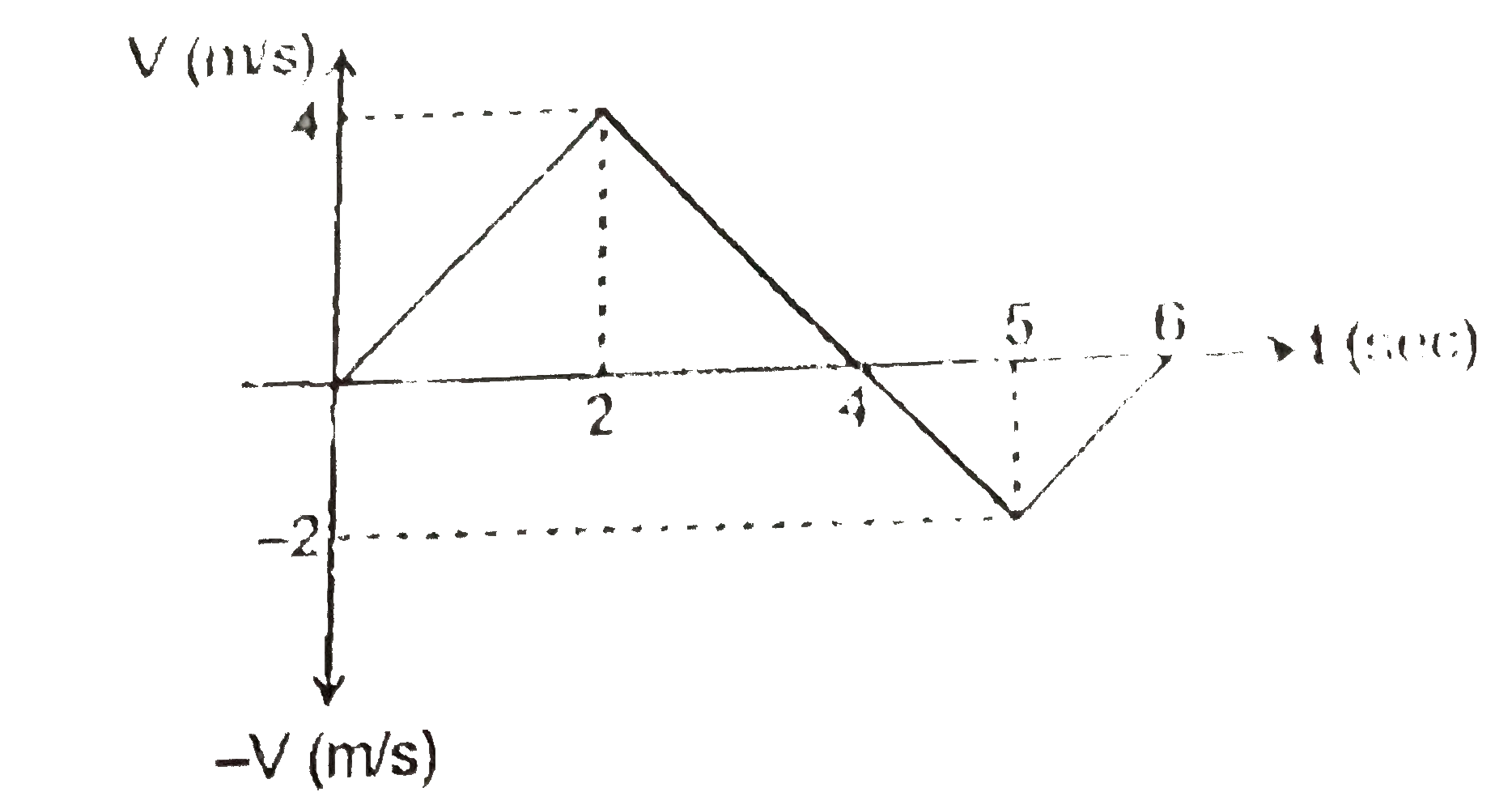
Average acceleration between (t = 0 sec) to (t = 6 sec)
View SolutionThe reation between the time t and position x for a particle moving on x-axis is given by t=px^(2)+qx , where p and q are constants. The relation between velocity v and acceleration a is as
View SolutionPosition of a particle moving along a straight line is given by x=2t^(2)+t . Find the velocity at t = 2 sec.
View SolutionThe velocity v of a particle at time t is given by v=at+bt+c where a, b and c are constant. The dimensions of a, b and c respectively are
View SolutionThe velocity of a moving particle is given by the equation v = (5 - t^(2)) The average acceleration of the particle between the 2nd and 3rd seconds is
View SolutionThe velocity of a particle is given by v=3+6(a1+a2t) where a, and an are constants and t is time. The acc. of particle is:
View SolutionThe displacement x of a particle at time t moving along a straight line path is given by x^(2) = at^(2) + 2bt + c where a, b and c are constants. The acceleration of the particle varies as
View SolutionThe position of a particle moving along a. straight line is given by x=2−5t+t3 The acceleration of the particle at t = 2 sec. is ...... Here x is in meter.
View SolutionThe velocity v of a particle at time t is given by v = a t + (b)/(t + c) , where a, b and c are constants. The dimensions of a, b and c are respectively
View Solution