एक सतत मुद्रण प्रक्रम में, कागज का रोल एक बेलनाकार क्रोड पर लिपटा हुआ है, जो एक नियत क्षैतिज अक्ष के अनुदिश घूर्णन करने के लिए स्वतंत्र है। जैसा कि चित्र में दिखाया गया है, कागज को एक नियत चाल v से प्रक्रम में खींचा जाता है। यदि किसी दिए गए समय पर | रोल पर कागज की त्रिज्या है और b कागज की मोटाई है, तो इस क्षण रोल का कोणीय त्वरण कितना है?

v2b2π2r3
शून्य क्योंकि v स्थिर है।
v2b2πr3
दी गई जानकारी से गणना नहीं की जा सकती
The correct Answer is:C
माना कि एक सतत मुद्रण प्रक्रम में कागज की कुल लंबाई l है। यदि r1 रोल की आंतरिक त्रिज्या है
तब, πr2−πr21−l×b…. (i)
और इस क्षण पर, u = rω ….. (ii)

समीकरण (i) का समय के सापेक्ष अवकलन करने पर,
π×2rdrdt=dldt.b
⇒drdt=−v.b2πr ...... (iii)
समीकरण (ii) का समय के सापेक्ष अवकलन करने पर,
⇒dvdt=r(dωdt)+ω(drdt)
⇒0=rα+ωdrdt(∵drdt is - ve)
⇒drdt=−rαω
⇒α=ωr(drdt).... (iv)
समीकरण (iii) और (iv) का उपयोग करने पर
vb.ω2πr2=u2b2πr3=α
Topper's Solved these Questions
Similar Questions
परमाण्विक हाइड्रोजन गैस का एक नमूना 100 nm और 200 nm के बीच तरंग दैर्ध्य वाले पराबैंगनी विकिरण के एक किरण-पुंज द्वारा विकिरणित होता है। यह मानते हुए कि परमाणु मूल अवस्था में हैं, संचरित किरण-पुंज में कम तीव्रता वाली तरंग दैर्ध्य कौन सी है?
View Solutionहाइड्रोजन स्पेक्ट्रम में Hλ रेखा की तरंग दैर्ध्य 656 nm है, जबकि एक दूरस्थ आकाशगंगा के स्पेक्ट्रम में Hλ रेखा की तरंग दैर्ध्य 706 nm है। पृथ्वी के सापेक्ष आकाशगंगा की अनुमानित चाल है:
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View SolutionThe sequence of folding a piece of square paper and the manner in which the folded paper has been cut is shown in the figure X, Y and Z. How would this paper look when unfolded? वर्गाकार कागज के एक टुकड़े को मोड़ने का क्रम और जिस तरह से मुड़ा हुआ कागज काट दिया गया है उसे चित्र X, Y और Z में दिखाया गया है। सीधा करने पर यह कागज़ कैसा दिखेगा?
View SolutionA paper is folded and cut as shown in the following figures. How will it appear when unfolded? एक कागज को मोड़ा और काटा जाता है जैसा कि निम्नलिखित आंकड़ों में दिखाया गया है। खुलने पर यह कैसे दिखाई देगा?
View SolutionA paper is folded and cut as shown in the following figures. How will it appear when unfolded? एक कागज को मोड़ा और काटा जाता है जैसा कि निम्नलिखित आंकड़ों में दिखाया गया है। खुलने पर यह कैसे दिखाई देगा?
View Solution27^@C पर एक अभिक्रिया के लिए K_p से K_c का अनुपात 24.63 L atm mol^(-1) है। यदि नियत दाब पर अभिक्रिया की ऊष्मा 98.8 kcal है, तो नियत आयतन पर अभिक्रिया की ऊष्मा (kcal में) क्या होगी?
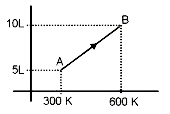
View Solutionचित्र में दर्शाये अनुसार एक आदर्श गैस के एक मोल को A→B अनुसार लिया गया है। प्रक्रम में निहित कार्य का परिमाण है: (R=253JmolK)
View Solutionनियत दाब पर एक आदर्श गैस की दी गई मात्रा के लिए निम्नलिखित में से कौन सा वक्र सही है?
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solutionएक स्थिर आयतन ऊष्मातापी में अणुभार 28 की एक गैस के 3.5 gको 298.0K पर ऑक्सीजन के अधिवाकय में जलाया गया था दहन प्रक्रम के कारण उष्मामापी के टप्प 298.0K से 298.45 K तक की वृद्धि पायी गयी दिया हुआ है की उष्मामापी की उष्मा धारिता 2.5 kg K^-1 है गैस के दहन की अन्थेलपी का संख्यात्मक मान में है
View Solutionदो द्रवों A और B के एक आदर्श मिश्रण को पिस्टन युक्त एक सिलेण्डर में रखा जाता है। पिस्टन को समतापीय रूप से खीचने पर द्रव का आयतन घटता है लेकिन वाष्प का आयतन बढ़ जाता है। द्रव की बहुत छोटी मात्रा शेष बचती है और वाष्प में A का मोल प्रभाज 0.4 होता है। यदि प्रायोगिक ताप पर P_(A)^(@) = 0.4 और P_(B)^(@) = 1.2 atm है, तो निम्नलिखित में से किस कुल दाब पर द्रव लगभग वाष्पीकृत हो जाता है?
View Solution
