द्रव्यमान m का एक गुटका A, बल नियतांक k की स्प्रिंग की मदद से छत से लटकने के बाद साम्यावस्था में है। m द्रव्यमान का गुटका B,u चाल के साथ गुटके A से टकराता है और इससे चिपक जाता है। u का वह मान क्या है, जिसके लिए स्प्रिंग केवल अपनी प्राकृतिक लंबाई प्राप्त करती है?

√6mg2k
√3mg2k
√2mg2k
√mg22k
The correct Answer is:A
माना संघट्ट के ठीक बाद संयुक्त निकाय का वेग u है, तब रेखीय संवेग संरक्षण का उपयोग करके हमें mv=2mu मिलता है,
⇒u=u2
स्प्रिंग का प्रारंभिक विस्तार
x=mgk
अब, यांत्रिक ऊर्जा संरक्षण का उपयोग करके हम प्राप्त करते हैं
122m(v)2+12kx2=2mgx
m(u24)+m2g22k=2m2g2k
u=√6mg2k
Related Playlists
Similar Questions
परमाण्विक हाइड्रोजन गैस का एक नमूना 100 nm और 200 nm के बीच तरंग दैर्ध्य वाले पराबैंगनी विकिरण के एक किरण-पुंज द्वारा विकिरणित होता है। यह मानते हुए कि परमाणु मूल अवस्था में हैं, संचरित किरण-पुंज में कम तीव्रता वाली तरंग दैर्ध्य कौन सी है?
08:32View Solutionहाइड्रोजन स्पेक्ट्रम में Hλ रेखा की तरंग दैर्ध्य 656 nm है, जबकि एक दूरस्थ आकाशगंगा के स्पेक्ट्रम में Hλ रेखा की तरंग दैर्ध्य 706 nm है। पृथ्वी के सापेक्ष आकाशगंगा की अनुमानित चाल है:
View Solutionचित्र में 60 ग्राम की प्लेट स्थिर एवं साम्यावस्था में है। द्रव्यमान m=30 ग्राम के एक कण को प्लेट से (4.5 mg)/k ऊंचाई से मुक्त करते हैं। कण प्लेट से चिपक जाता है। टक्कर-अंतराल को नगण्य मानते हुए वह समय अंतराल ज्ञात करों जिसमें कण जब प्लेट से टकराता है तथा स्प्रिंग महत्तम संपीड़ित होती है। स्पि्रंग का बल नियतांक 100 N/m है। समय की गणना Xπms (मिली-सेकण्ड) के रूप में ज्ञात करो तथा X का मान उत्तर पुस्तिका में लिखिए।
 03:25View Solution
03:25View Solutionगहरी कुंई से पानी खींचने की सुविधा के लिए ____ का उपयोग किया जाता है।
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solutionक्रोमिक अम्ल की मदद से फीनॉल के ऑक्सीकरण द्वारा प्राप्त उत्पाद का IUPAC नाम है:
View Solutionएक द्रव, जल में अमिश्रणीय है जो कि 0.983 atm के दाब और 95.2^(@)C पर भाप आसवित है। आसुत में जल के प्रति ग्राम में उपस्थित द्रव का द्रव्यमान क्या है। द्रव का मोलर द्रव्यमान 134.3 g/mol है और जल का वाष्प दाब 0.84 atm है। साथ ही, शुद्ध द्रव का वाष्प दाब 0.143 atm है।
View Solutionनिम्नलिखित में से अभिकारकों के किस समूह का उपयोग फेनोल से पेरासिटामोल के निर्माण के लिए किया जाता है
View Solutionऐडिनिन न्यूक्लिक अम्ल के न्यूक्लियोटाइडों के निर्माण में शामिल दो प्यूरीन क्षारों में से एक है। ऐडिनिन का अणुसूत्र CxHxNx होता है, तो 'x' का मान है
View Solutionएक निश्चित बफर विलयन में X^- और HX की समान सांद्रता उपस्थित है। HX के लिए K_a का मान 10^(-8) है। बफर की pH क्या होगी?
View Solutionरेडियो नाभिक 90234Th के दो क्रमिक β -क्षय के बाद एक -क्षय के माध्यम से एक नया रेडियो नाभिक प्राप्त किया जाता है। परिणामी रेडियो नाभिक का परमाणु क्रमांक और द्रव्यमान संख्या क्रमश: है:
View Solutionबोश प्रक्रम का उपयोग हाइड्रोजन गैस के उत्पादन के लिए किया जाता है, दी गई गैस में से किस गैस का उपयोग इसके लिए किया जाता है
View Solutionकैल्सियम के निर्माण के लिए निम्नलिखित में से किस प्रक्रम का उपयोग किया जाता है?
View Solution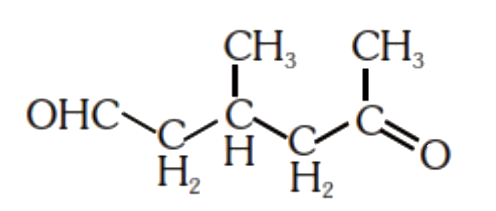
उपरोक्त संरचना का एक एकल यौगिक निम्नलिखित में से कौनसे चक्रीय यौगिक के ओजोनी अपघटन से प्राप्त किया जाता है?View Solutionअमोनियम मोलिब्डेट के साथ फॉस्फेट मूलक की अभिक्रिया से कौन से रंग का अवक्षेप प्राप्त होता है
View Solutionगतिक साम्य में दोनों दिशाओं में अभिक्रिया एक ही दर से होती है और साम्य के दोनों ओर द्रव्यमान किसी भी परिवर्तन से नहीं गुजरता है। यह अवस्था केवल तभी प्राप्त की जा सकती है जब ΔGका मान
View Solution


