If look inside a real piano , you'll see that the assumption made in part (b) of Illustration 7.31 is only partially true . The strings are not likely to have the length of the A string is only 64% of the length of the C string . What is the ratio of their tensions ?
To find the ratio of the tensions in the A and C strings of a piano, we can use the relationship between frequency, tension, length, and linear mass density of the strings. Here’s a step-by-step solution:
Step 1: Understand the relationship between frequency, tension, and length
The frequency of a vibrating string is given by the formula:
f=12L√Tμ
where:
- f is the frequency,
- L is the length of the string,
- T is the tension in the string,
- μ is the linear mass density of the string.
Step 2: Set up the equations for both strings
For string A (frequency fA=440 Hz):
fA=12LA√TAμ
For string C (frequency fC=262 Hz):
fC=12LC√TCμ
Step 3: Express the lengths in terms of each other
We know that the length of string A is 64% of the length of string C:
LA=0.64LC
Step 4: Substitute the lengths into the frequency equations
Substituting LA into the equation for string A:
fA=12(0.64LC)√TAμ
Step 5: Divide the equations for the two strings
Now, divide the equation for string A by the equation for string C:
fAfC=LCLA⋅√TATC
Substituting the known values:
440262=LC0.64LC⋅√TATC
Step 6: Simplify the equation
The LC cancels out:
440262=10.64⋅√TATC
Step 7: Isolate the tension ratio
Rearranging gives:
√TATC=440262⋅0.64
Step 8: Square both sides
Squaring both sides results in:
TATC=(440262⋅0.64)2
Step 9: Calculate the ratio
Calculating the right-hand side:
1. Calculate 440262≈1.679.
2. Multiply by 0.64 to get approximately 1.073.
3. Square this result: (1.073)2≈1.152.
Thus, we find:
TATC≈1.16
Final Answer
The ratio of the tensions in string A to string C is approximately:
TATC≈1.16
The frequency of a vibrating string is given by the formula:
f=12L√Tμ
where:
- f is the frequency,
- L is the length of the string,
- T is the tension in the string,
- μ is the linear mass density of the string.
For string A (frequency fA=440 Hz):
fA=12LA√TAμ
fC=12LC√TCμ
We know that the length of string A is 64% of the length of string C:
LA=0.64LC
Substituting LA into the equation for string A:
fA=12(0.64LC)√TAμ
Now, divide the equation for string A by the equation for string C:
fAfC=LCLA⋅√TATC
440262=LC0.64LC⋅√TATC
The LC cancels out:
440262=10.64⋅√TATC
Rearranging gives:
√TATC=440262⋅0.64
Squaring both sides results in:
TATC=(440262⋅0.64)2
Calculating the right-hand side:
1. Calculate 440262≈1.679.
2. Multiply by 0.64 to get approximately 1.073.
3. Square this result: (1.073)2≈1.152.
TATC≈1.16
The ratio of the tensions in string A to string C is approximately:
TATC≈1.16
Similar Questions
A string of linear mass density 0.5gcm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end. The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20cms−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string ?

View SolutionTwo uniform strings AandB made of steel are made to vibrate under the same tension. If the first overtone of A is equal to the second overtone of B and if the radius of A is twice that of B, the ratio of the lengths of the strings is
View SolutionA sinusoidal transverse wave travel on a string. The string has length 8.00m and mass 6.00g. The wave speed is 30.0m/s and the wavelength is 0.200m. (a) If the wave is to have an average power of 50.0W, what must be the amplitude of the wave? (b) For the same string, if the ampitude and wavelength are the same as in part (a) what is the average power for the wave if the tension is increased such that the wave speed is doubled?
View SolutionA middle C string on a piano has a fundamental frequency of 262Hz, and the A note has fundamental frequency of 440Hz. (a) Calculate the frequencies of the next two harmonics of the C string. (b) If the strings for the A and C notes are assumed to have the same mass per unit length and the same length, determine the ratio of tension in the two strings.
View SolutionTwo identical piano strings of length 0.750m are each tunned exactly to 440Hz. The tension in one of the strings is then increased by 1.0%. If they are now struck , what is the beat frequency between the fundamental of the two strings ?
View Solution
A uniform rod of mass m and length l is held horizontally by two vertical strings of negligible mass, as shown in the figure.
(a). Immediately after the right string is cut, what is the linear acceleration of the end of the rod?
(b). Of the middle of the rod?
(c). Determine the tension in the left string immediately after the right string is cut.
View SolutionA vibrating string of certain length l under a tension T resonates with a mode corresponding to the first overtone (third harmonic ) of an air column of length 75cm inside a tube closed at one end. The string also generates 4beats/s with a tuning fork of frequency n . Now when the tension of the string is slightly increased the number of beats reduces to 2 per second. Assuming the velocity of sound in air to 340m/s , the frequency n the tuning fork in HZ is
(a) 344
(b) 336
(c ) 117.3
(d) 109.3
View SolutionThe diagram alongside shows a pulley arrangement.
(a) Name the pulleys A and B.
(b) In the diagram, mark the direction of tension on each strand of string.
(c) What is the purpose of the pulley B?
(d) If the tension is T, deduce the relation between
T and E
(e) What is the velocity ratio of the arrangement ?
(f) Assuming that the efficiency of the system is 100%, what is the mechanical advantage ?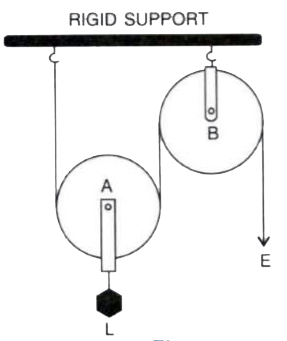
View SolutionTwo identical piano strings of length 0.750 m are each, tuned exactly to 500 Hz. The tension in one of the strings is then increased by 21%. If they are now struck, what is the beat frequency between the fundamental mode of the two strings?
View SolutionFigure 7.88 shows a stretched string of length L and pipes of length L,2L,L/2andL/2 in options (a) , (b), (c ) and (d) respectively . The string 's tension is adjusted until the speed of waves on the string equals the speed of sound waves in the air . The fundamental mode of oscillation is the set up on the string . In which pipe will the sound produced by the string cause resonance ?

View Solution
