The graph between log R and log A where R is the nuclear radius and A is the mass number is.




The correct Answer is:A
Step by step video & image solution for The graph between log R and log A where R is the nuclear radius and A is the mass number is. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.215videos
NUCLEAR PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.315videos
NUCLEAR PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Integer type3videos
NUCLEAR PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Integer Type4videos
PHOTOELECTRIC EFFECT
Similar Questions
The graph between logk versus 1/T is a straight line.
View SolutionThe graph between log t1/2 and log a at a given temperature is
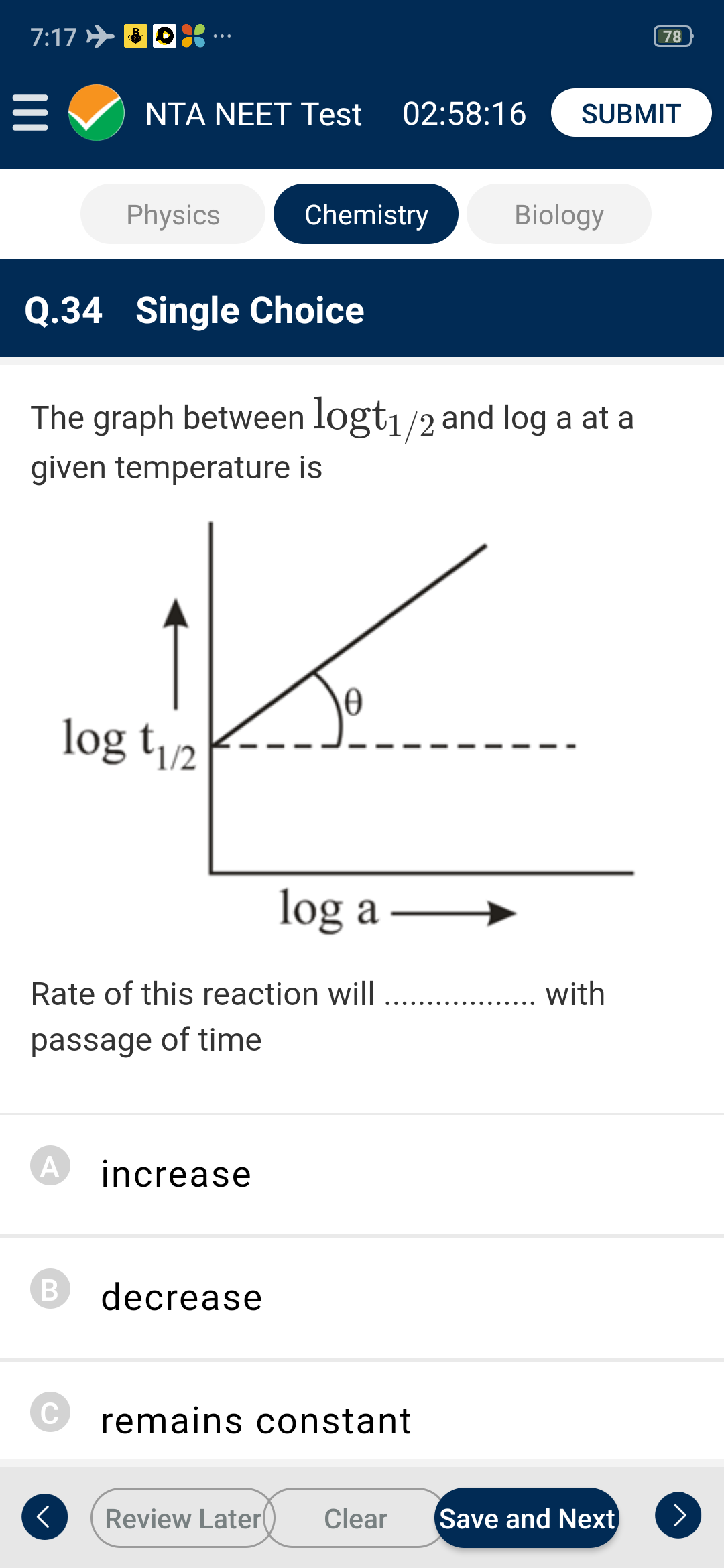
Rate of this reaction will …….with passage of timeView SolutionThe slope of the graph between log P and log V at constant temperature for a given mass of gas is
View SolutionThe graph of 1n(RR0) versus 1nA(R=radius of a nucleus and A= its mass number) is
View SolutionWhat is the type of graph between log P and log V at constant temperature?
View SolutionFollowing is the graph between logT50 and loga (a= initial concentration) for a given reaction at 27∘C. Hence order is
 View Solution
View SolutionA graph between logt12 and log a (abscissa), a being the initial concentration of A in the reaction For reaction A→Product, the rate law is :
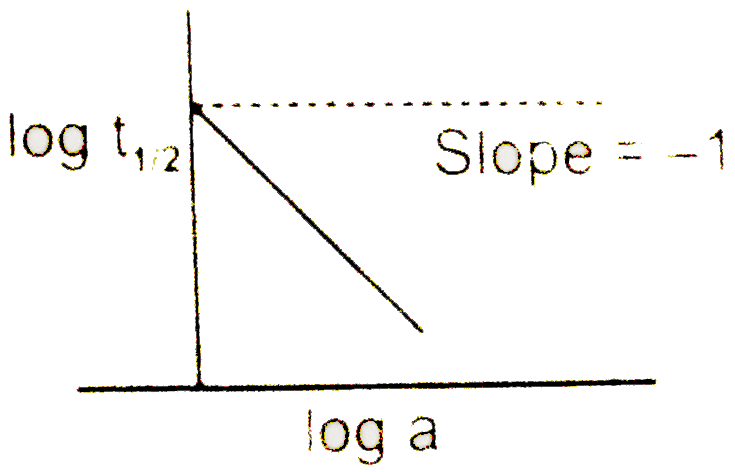 View Solution
View SolutionA graph between logt12 and log a (abscissa), a being the initial concentration of A in the reaction For reaction A→Product, the rate law is :
 View Solution
View SolutionFollowing is the graph between logt1/2 and loga (a initial concentration) for a given reaction at 300K

Find the order of reaction.View Solutionfrom the relation R=R0A1/3, where R0 is a constant and A is the mass number of a nucleus, show that the nuclear matter density is nearly constant (i.e., independent of A ).
View Solution
