One of the forces acting on the particle is conservative, then
Its work is zero when the particle moves exactly once around any closed path.
its work equals the change in the kinetic energy of the particle
Then that particular force must be constant.
Its work depends on the end points of the motion, not on the path between.
The correct Answer is:A, D
Only the following statement are true from definition of a conservative force.
Its work is zero when the particle moves exactly once around any closed path.
Its work depends on the end point of the motion, not on the path between.
Similar Questions
One of the forces acting on a particle is conservative then which of the following statement (s) are true about this conservative force
View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region

View SolutionA particle is acted upon by only a conservative force F=(7ˆi−6ˆj) N (no other force is acting on the particle). Under the influence of this force particle moves from (0, 0) to (-3m, 4m) then
View SolutionSTATEMENT-1: Work done by the net force acting on a particle is equal to the change in its kinetic energy.
STATEMENT-2: Change in potential energy is always equal to the work done by external forces.
STATEMENT-3: Work energy theorem is not applicable, if the work is done by the non-conservative forces
View SolutionThe momentum of a moving particle given by p=tlnt. Net force acting on this particle is defined by equation F=dpdt. The net force acting on the particle is zero at time
View SolutionA charged is moving with constant velocity parallel to a horizontal current carrying long wire. The direction of velocity of that particle and the current are same. If the force acting on the particle are only magnetic force due to wire and gravitational force due to earth, then the particle :
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
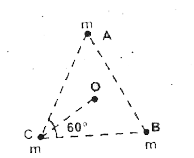
Force acting on particle C, due to particle A and B
View SolutionStatement 1: A charged particle undergoes non-rectilinear motion in a constant magnetic field. The only force acting on the particle is the magnetic force. Then kinetic energy of this particle remains constant but momentum of the particle does not remains constant.
Statement 2: A force that always acts on the particle in direction perpendicular to its velocity does no work on the particle. But whenever a force acts on the particle, momentum of the particle does not remains constant.
View SolutionAssertion Centripetel force (mv2)/(R) acts on a particle rotating in a circle.
Reason Summation of net force acting on the particle is equal to (mv2)/(R) in the above case.
View SolutionIf the resultant of all the external forces acting on a system of particles is zero. Then from an inertial frame, one can surely say that
View Solution
