A spring balance and a physical balance are kept in a lift. In these balance equal masses are placed. If now the lift starts moving upward with constant acceleration, then.
the reading of spring balance will increase and the equilibrium position of the physical balance will disturb
the reading of spring balance will remain unchanged and physical balance will remain in equilibrium
the reading of spring balance will decrease and physical balance will remain in equilibrium
the reading of spring balance will increase and the phusical balance will remain in equilibrium
The correct Answer is:D
To solve the problem, we need to analyze the behavior of both the spring balance and the physical balance when the lift is moving upward with a constant acceleration.
1. Understanding the Forces Acting on the Mass:
- When the lift accelerates upwards with an acceleration A, the forces acting on the mass M placed on the balances are:
- The gravitational force acting downwards: Fg=mg
- The normal force acting upwards: N
2. Calculating the Normal Force on the Spring Balance:
- The net force acting on the mass when the lift is accelerating upwards can be expressed using Newton's second law:
Fnet=ma
- The normal force N must counteract both the weight of the mass and provide the necessary force for the upward acceleration:
N−mg=ma
- Rearranging gives:
N=mg+ma=m(g+a)
- Thus, the reading on the spring balance, which measures the normal force, will increase to m(g+a).
3. Analyzing the Physical Balance:
- A physical balance compares the weights of two masses. If equal masses are placed on both sides of the balance, the forces acting on them are the same:
- For both masses, the normal force is N=m(g+a).
- Since both sides experience the same normal force, the physical balance will remain in equilibrium.
4. Conclusion:
- The reading on the spring balance increases because the normal force has increased.
- The physical balance remains in equilibrium because the normal forces on both sides are equal.
Final Answer:
- The reading of the spring balance will increase, and the physical balance will remain in equilibrium. Therefore, the correct option is:
Option 4: The reading of the spring balance will increase, and the physical balance will remain in equilibrium.
- When the lift accelerates upwards with an acceleration A, the forces acting on the mass M placed on the balances are:
- The gravitational force acting downwards: Fg=mg
- The normal force acting upwards: N
- The net force acting on the mass when the lift is accelerating upwards can be expressed using Newton's second law:
Fnet=ma
- The normal force N must counteract both the weight of the mass and provide the necessary force for the upward acceleration:
N−mg=ma
- Rearranging gives:
N=mg+ma=m(g+a)
- Thus, the reading on the spring balance, which measures the normal force, will increase to m(g+a).
- A physical balance compares the weights of two masses. If equal masses are placed on both sides of the balance, the forces acting on them are the same:
- For both masses, the normal force is N=m(g+a).
- Since both sides experience the same normal force, the physical balance will remain in equilibrium.
- The reading on the spring balance increases because the normal force has increased.
- The physical balance remains in equilibrium because the normal forces on both sides are equal.
- The reading of the spring balance will increase, and the physical balance will remain in equilibrium. Therefore, the correct option is:
Option 4: The reading of the spring balance will increase, and the physical balance will remain in equilibrium.
Similar Questions
A block of mass m is placed on weighing machine and it is also attached with a spring balance. The whole system is placed in a lift as shown in figure. Left is moving with constant acceleration 10m/s2 in upward direction. The reading of the weighing machine is 500 N and the reading of spring balance is 300 N. Find the actual mass of the block in kg. (Takr g=10m/s2)

View SolutionA block of wood floats in a bucket of water placed in a lift. Will the block sink more or less if the lift starts accelerating up?
View SolutionA wooden block is floating on water kept in a beaker. 40% of the block is above the water surface. Now the beaker is kept inside a lift that starts going upward with acceleration equal to g/2. The block will then
View SolutionA lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string T1. Two masses of m1andm2 are connected with inextensible light string and tension in this string T2 as shown in figure. Read the questionbs carefully and answer
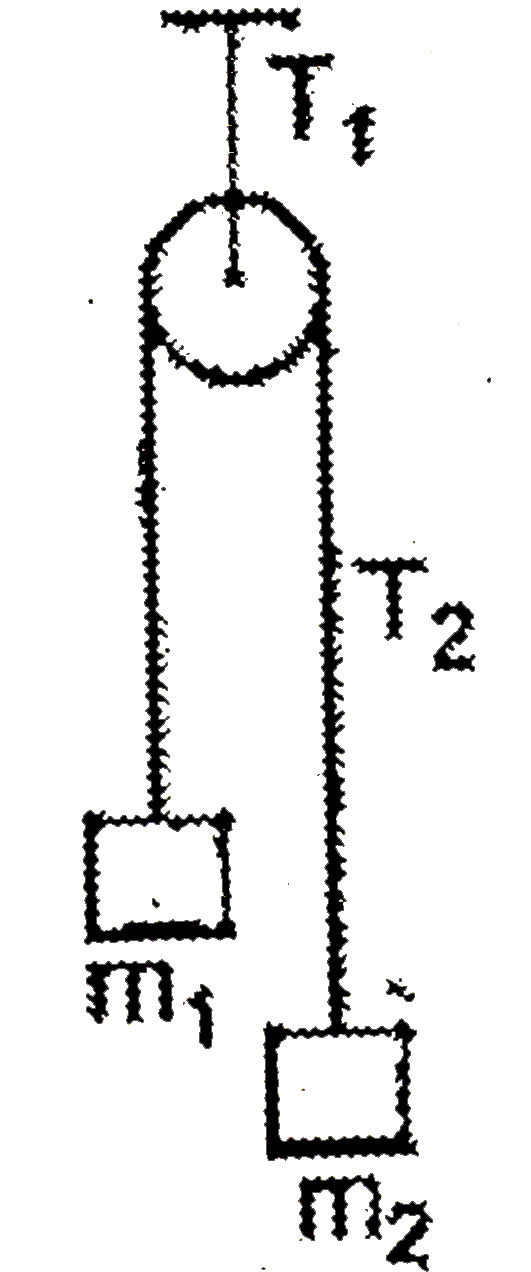
If m1=m2andm1 is moving at a certain instant with velocity v upward with respect to lift and the lift is moving in upward direction with constant acceleration (a<g) then speed of m2 with respect to lift :
View SolutionThe time period of a simple pendulum measured inside a stationary lift is found to be T . If the lift starts accelerating upwards with an acceleration g/3, the time period is
View SolutionA body of mass 50 kg is hung by a spring balance in a lift. Calculate the reading of the balance when :
The lift is ascending with an acceleration of 2m/s2.
View SolutionTime period of a spring pendulum when lift moves downward with constant velocity v is T second. When the lift moves upward with constant acceleration=g3 , the time period will be

View SolutionThe time period of a simple pendulum inside a stationary lift is √5 s. What will be the time period when the lift moves upward with an acceleration g4?
View SolutionA spring balance is attached to the ceiling of a lift. A man hangs his bag on the spring and the spring reads 49N, when the lift is stationary. If the lift moves downward with an acceleration of 5m/22, the reading of the spring balance will be
View SolutionA spring balance is attached to the ceiling of a lift. A man hangs his bag on the spring and the spring reads 49N, when the lift is stationary. If the lift moves downward with an acceleration of 5m/22, the reading of the spring balance will be
View Solution