A particle is moving on the x-axis. If initial velocity u>0, and acceleration a<0 and a is constant then number of possible calues of the time for which the particle is at distance d from its starting point may be:
one
two
three
four
The correct Answer is:A, B, C
To solve the problem, we need to analyze the motion of a particle moving along the x-axis with an initial velocity u>0 and a constant negative acceleration a<0. We are interested in finding the number of possible times the particle can be at a distance d from its starting point.
1. Understanding the Motion:
The particle starts from the origin (0,0) with an initial velocity u and is decelerating due to negative acceleration a. The motion can be described by the kinematic equation:
x=ut+12at2
where x is the position of the particle at time t.
2. Setting Up the Equation:
We want to find the times t when the particle is at a distance d from the starting point, which gives us the equation:
d=ut+12at2
Rearranging this, we have:
12at2+ut−d=0
3. Analyzing the Quadratic Equation:
This is a quadratic equation in the form At2+Bt+C=0, where:
- A=12a
- B=u
- C=−d
4. Finding the Discriminant:
The number of solutions (i.e., possible times t) depends on the discriminant D of the quadratic equation:
D=B2−4AC=u2−4(12a)(−d)=u2+2ad
5. Determining the Number of Solutions:
- If D>0, there are two distinct solutions for t.
- If D=0, there is one solution for t.
- If D<0, there are no real solutions for t.
6. Conditions for D:
Since a<0, the term 2ad is negative. Therefore, the value of u2+2ad can be analyzed:
- If u2>−2ad, then D>0 (two solutions).
- If u2=−2ad, then D=0 (one solution).
- If u2<−2ad, then D<0 (no solutions).
7. Conclusion:
The possible values for the number of times the particle can be at distance d from the starting point are:
- 1 time (if it just touches the distance d),
- 2 times (if it crosses the distance d while moving forward and then backward),
- 3 times (if it moves past d and returns).
Thus, the final answer is that the number of possible values of time for which the particle is at distance d from its starting point may be 1, 2, or 3.
The particle starts from the origin (0,0) with an initial velocity u and is decelerating due to negative acceleration a. The motion can be described by the kinematic equation:
x=ut+12at2
where x is the position of the particle at time t.
We want to find the times t when the particle is at a distance d from the starting point, which gives us the equation:
d=ut+12at2
Rearranging this, we have:
12at2+ut−d=0
This is a quadratic equation in the form At2+Bt+C=0, where:
- A=12a
- B=u
- C=−d
The number of solutions (i.e., possible times t) depends on the discriminant D of the quadratic equation:
D=B2−4AC=u2−4(12a)(−d)=u2+2ad
- If D>0, there are two distinct solutions for t.
- If D=0, there is one solution for t.
- If D<0, there are no real solutions for t.
Since a<0, the term 2ad is negative. Therefore, the value of u2+2ad can be analyzed:
- If u2>−2ad, then D>0 (two solutions).
- If u2=−2ad, then D=0 (one solution).
- If u2<−2ad, then D<0 (no solutions).
The possible values for the number of times the particle can be at distance d from the starting point are:
- 1 time (if it just touches the distance d),
- 2 times (if it crosses the distance d while moving forward and then backward),
- 3 times (if it moves past d and returns).
Similar Questions
A particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
total distance covered by the particle is
View SolutionA particle starts from rest. Its acceleration is varying with time as shown in the figure. When the particle comes to rest, its distance from its starting point is

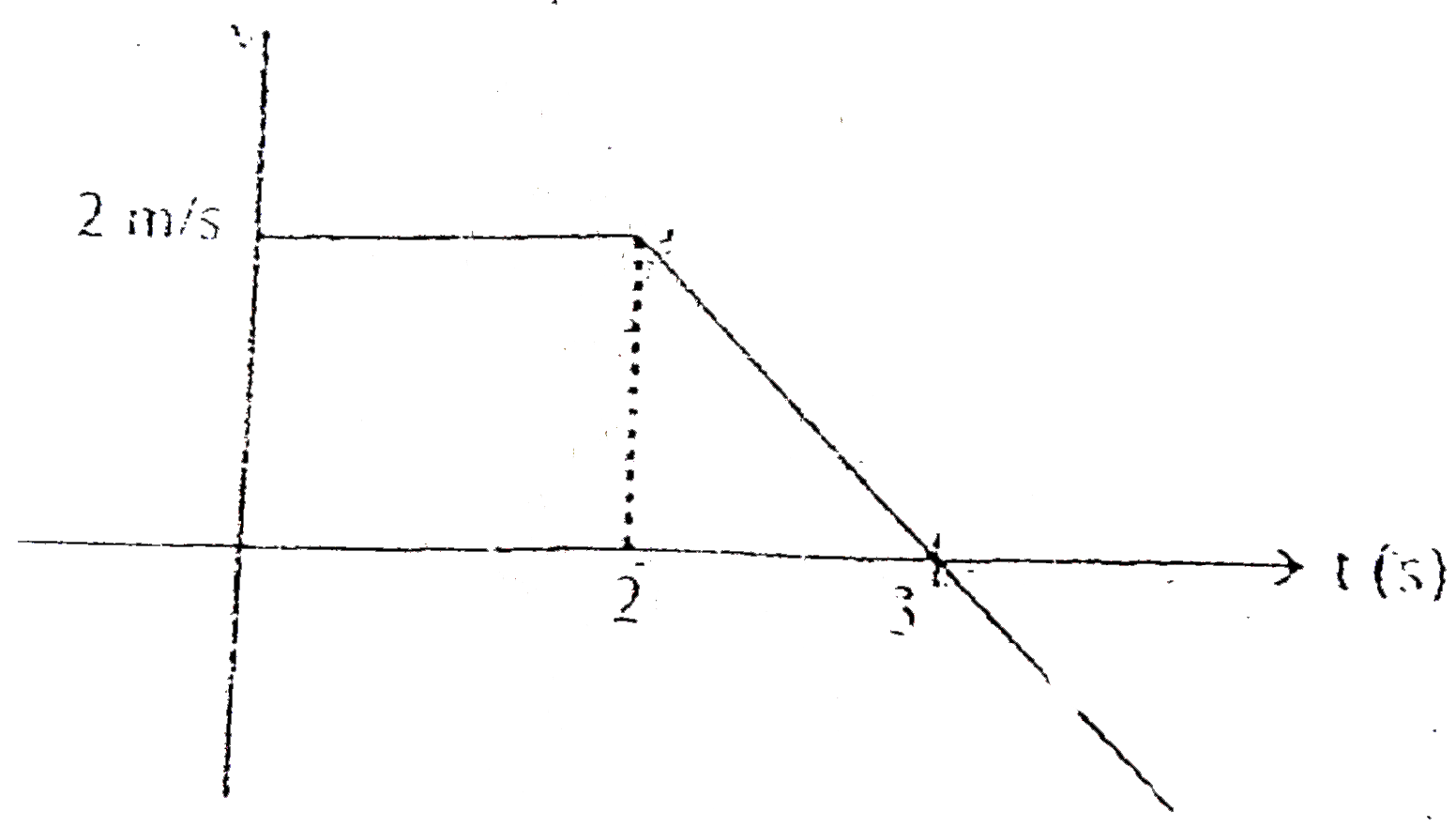
View SolutionA particle is moving on X−axis. Its velocity time graph is given in the figure. Find distance travelled by the particle in 5sec.
View SolutionA particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
Velocity of particle at time is :
View SolutionA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionA particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
View SolutionA particle is moving along the x-axis with an acceleration a = 2x where a is in ms–2andx is in metre. If the particle starts from rest at x=1 m, find its velocity when it reaches the position x = 3.
View SolutionA particle is moving along x-axis with constant acceleration. At t=0, the particle is at x=3m and dxdt=+4m/s. The maximum value of x co-ordiante of the particle is observed 2 seconds later. Starting from t=0 sec, after what time, particle reaches its initial position again?
View SolutionA particle moves rectilinearly with initial velocity u and constant acceleration a. Find the average velocity of the particle in a time interval from t=0 to t=t second of its motion.
View SolutionA particle moves aling x-axis with an initial speed v0=5ms−1. If its acceleration varies with with time asshown in a−t graph in .
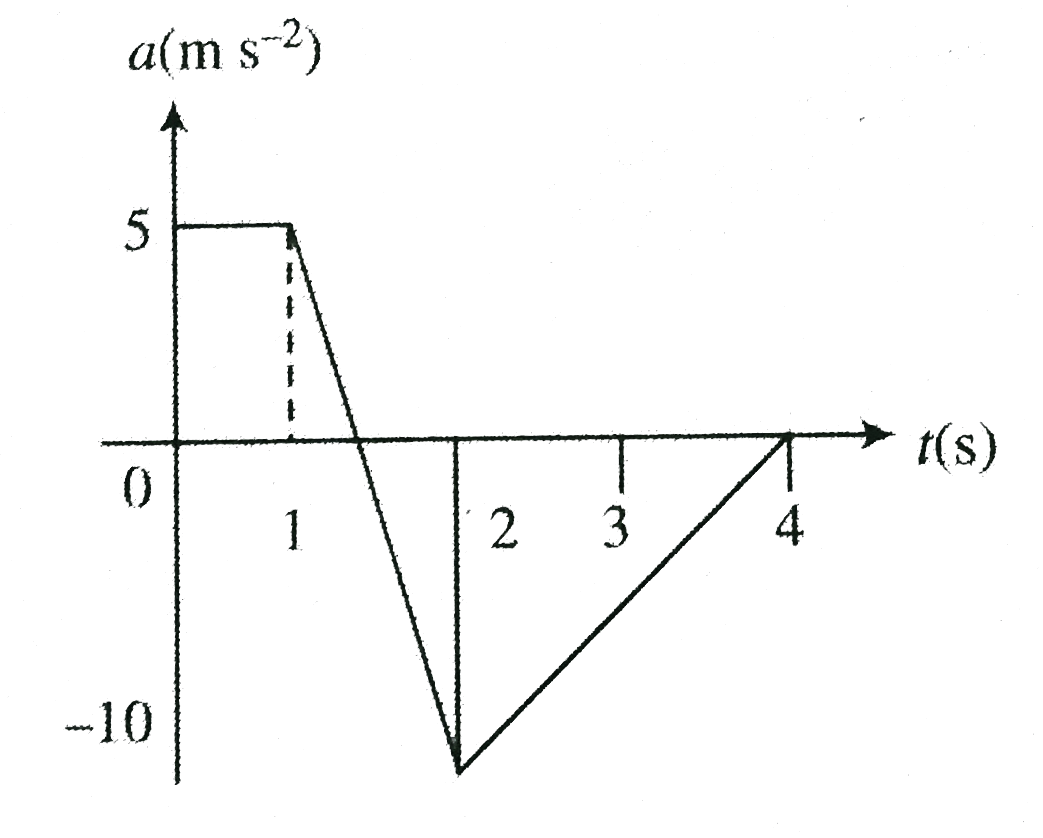 .
.
a. Find the time when the particle starts moving along - x direction
View Solution
